Going beyond p-convolutions to learn grayscale morphological operators
Paper and Code
Feb 19, 2021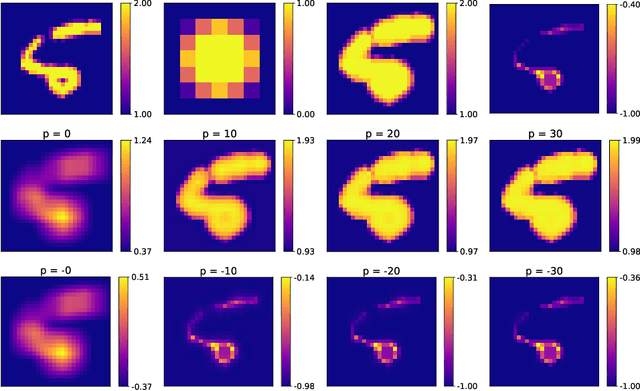
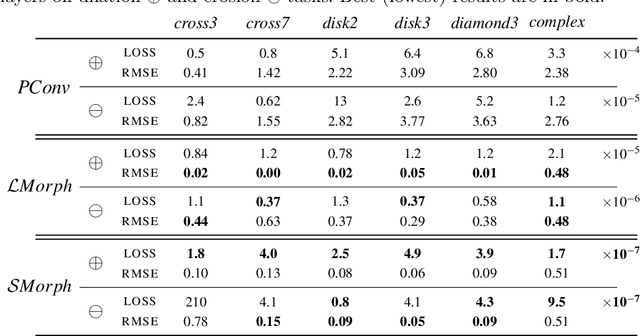
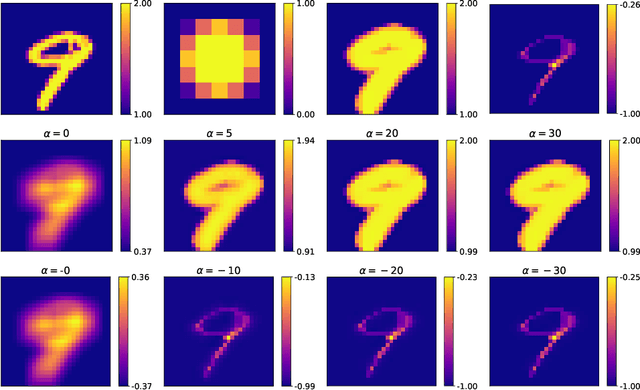
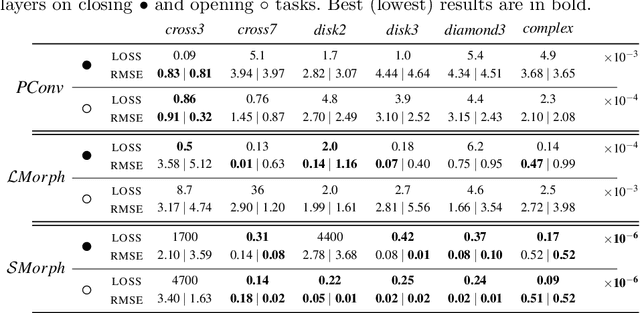
Integrating mathematical morphology operations within deep neural networks has been subject to increasing attention lately. However, replacing standard convolution layers with erosions or dilations is particularly challenging because the min and max operations are not differentiable. Relying on the asymptotic behavior of the counter-harmonic mean, p-convolutional layers were proposed as a possible workaround to this issue since they can perform pseudo-dilation or pseudo-erosion operations (depending on the value of their inner parameter p), and very promising results were reported. In this work, we present two new morphological layers based on the same principle as the p-convolutional layer while circumventing its principal drawbacks, and demonstrate their potential interest in further implementations within deep convolutional neural network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge