Global, Unified Representation of Heterogenous Robot Dynamics Using Composition Operators
Paper and Code
Jul 30, 2022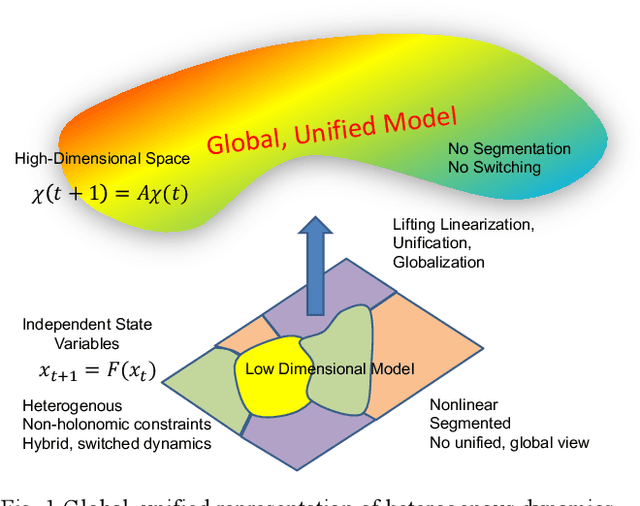
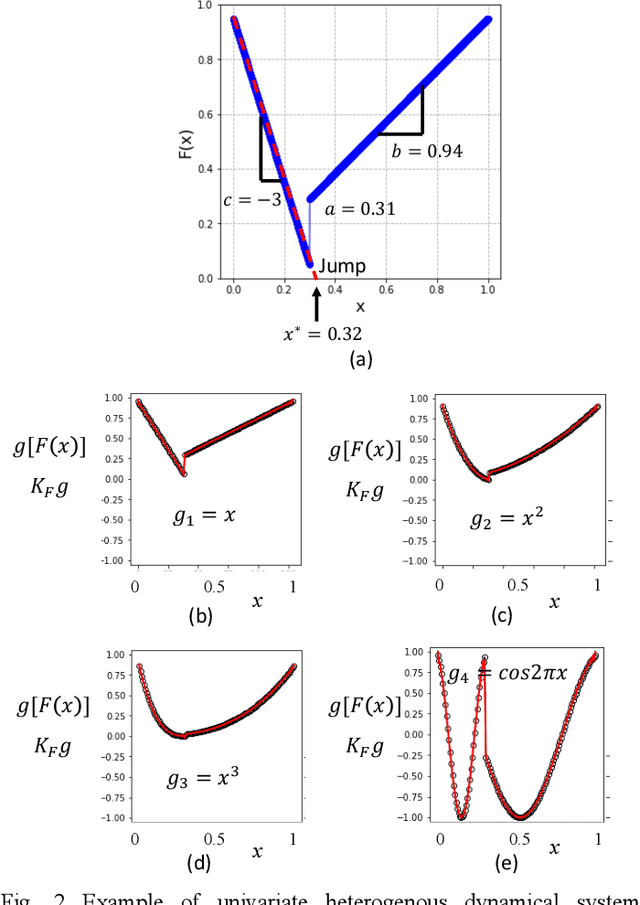
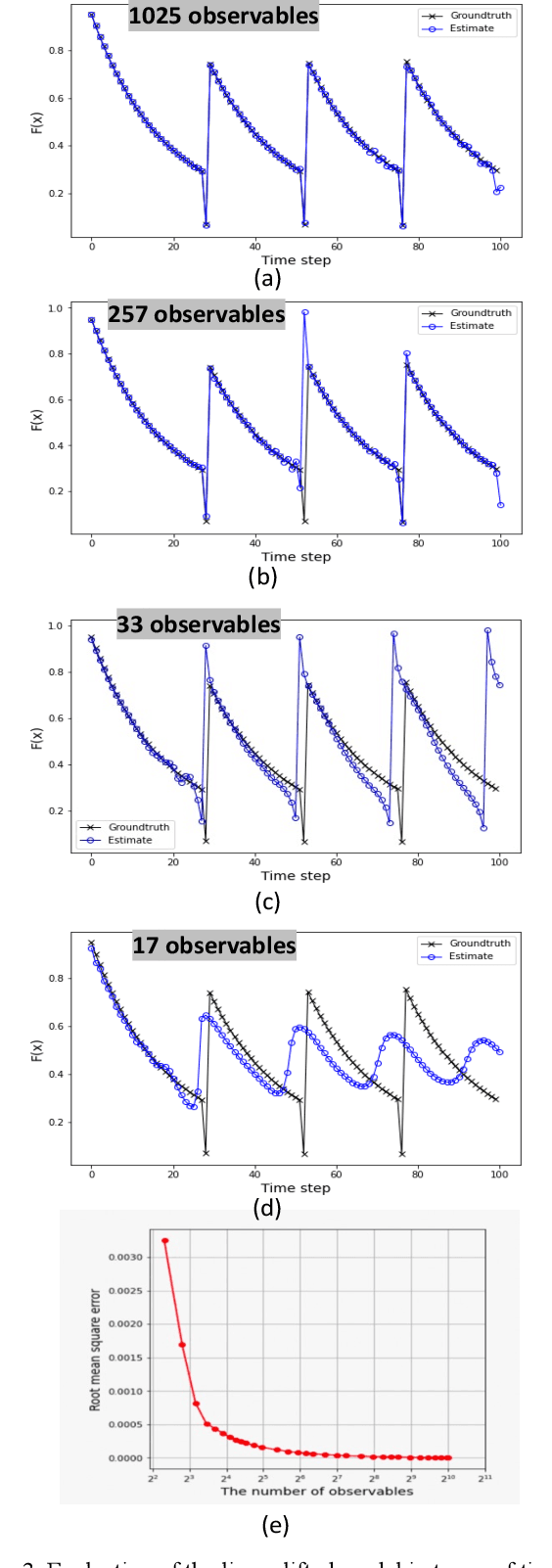
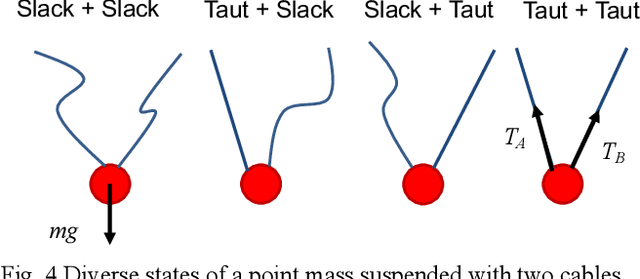
The complexity of robot dynamics often pertains to the hybrid nature of dynamics, where governing dynamic equations consist of heterogenous equations that are switched depending on the state of the system. Legged robots and manipulator robots experience contact-noncontact discrete transitions, causing switching of governing equations. Analysis of these robot systems have been a challenge due to the lack of a global, unified model that is amenable to analysis of the global behaviors. Composition operator theory has the potential to provide a global, unified representation of those heterogenous dynamical systems. It is expected that, if the theory is applicable, those fundamentally challenging robotics systems can be treated as linear dynamical systems in a lifted space. The current work addresses under which conditions a unified linear representation exists in a global sense for a class of heterogenous dynamical systems and how the theory can be applied to those robotics problems. First, a kernel representation of composition operators is obtained, and conditions required for converting the kernel representation to a linear state transition equation are established. This analysis results in an algorithm to convert a class of heterogenous systems including hybrid and switched systems directly to a global, unified linear model. Unlike prevalent data-driven methods and Dynamic Mode Decomposition, where results can vary depending on numerical data, the proposed method does not require numerical simulation of the original dynamics. The implication of the new method and its impact upon robotics are discussed. A few examples validate and demonstrate the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge