Generative Lines Matching Models

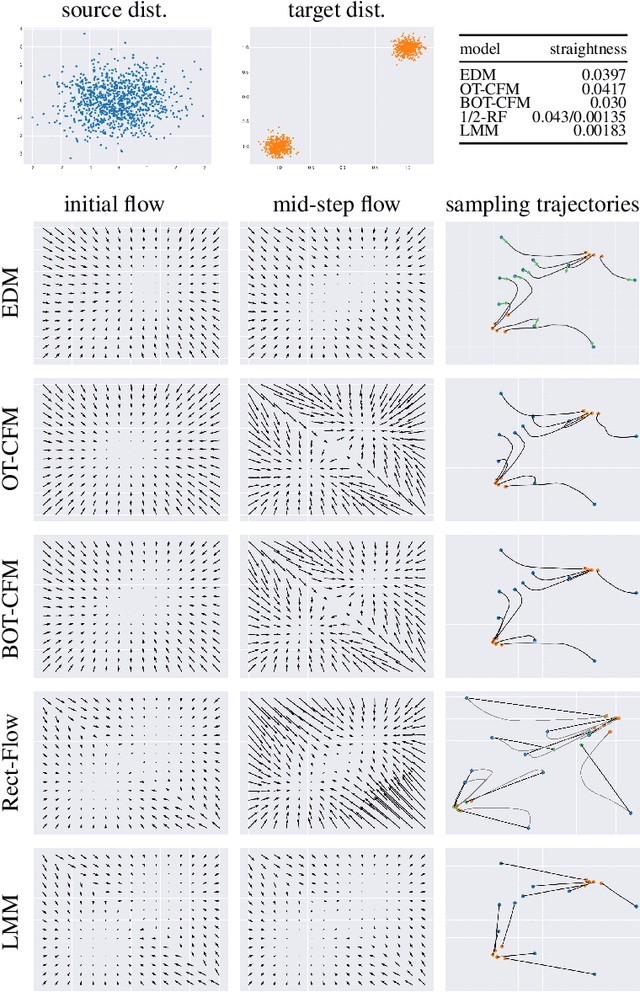
In this paper we identify the source of a singularity in the training loss of key denoising models, that causes the denoiser's predictions to collapse towards the mean of the source or target distributions. This degeneracy creates false basins of attraction, distorting the denoising trajectories and ultimately increasing the number of steps required to sample these models. We circumvent this artifact by leveraging the deterministic ODE-based samplers, offered by certain denoising diffusion and score-matching models, which establish a well-defined change-of-variables between the source and target distributions. Given this correspondence, we propose a new probability flow model, the Lines Matching Model (LMM), which matches globally straight lines interpolating the two distributions. We demonstrate that the flow fields produced by the LMM exhibit notable temporal consistency, resulting in trajectories with excellent straightness scores. Beyond its sampling efficiency, the LMM formulation allows us to enhance the fidelity of the generated samples by integrating domain-specific reconstruction and adversarial losses, and by optimizing its training for the sampling procedure used. Overall, the LMM achieves state-of-the-art FID scores with minimal NFEs on established benchmark datasets: 1.57/1.39 (NFE=1/2) on CIFAR-10, 1.47/1.17 on ImageNet 64x64, and 2.68/1.54 on AFHQ 64x64. Finally, we provide a theoretical analysis showing that the use of optimal transport to relate the two distributions suffers from a curse of dimensionality, where the pairing set size (mini-batch) must scale exponentially with the signal dimension.