Generation of Conservative Dynamical Systems Based on Stiffness Encoding
Paper and Code
Nov 02, 2024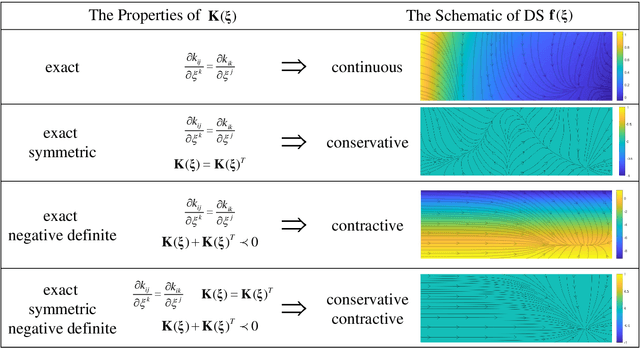
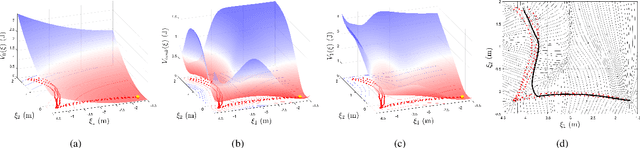
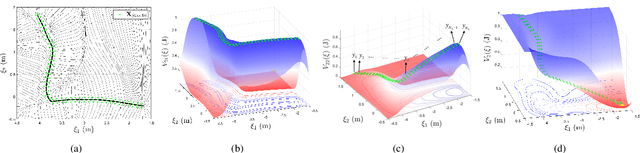
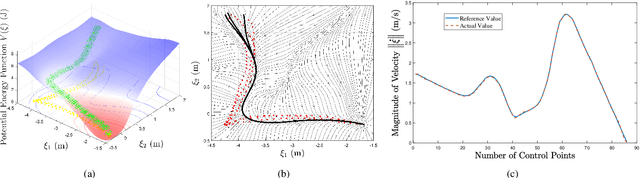
Dynamical systems (DSs) provide a framework for high flexibility, robustness, and control reliability and are widely used in motion planning and physical human-robot interaction. The properties of the DS directly determine the robot's specific motion patterns and the performance of the closed-loop control system. In this paper, we establish a quantitative relationship between stiffness properties and DS. We propose a stiffness encoding framework to modulate DS properties by embedding specific stiffnesses. In particular, from the perspective of the closed-loop control system's passivity, a conservative DS is learned by encoding a conservative stiffness. The generated DS has a symmetric attraction behavior and a variable stiffness profile. The proposed method is applicable to demonstration trajectories belonging to different manifolds and types (e.g., closed and self-intersecting trajectories), and the closed-loop control system is always guaranteed to be passive in different cases. For controllers tracking the general DS, the passivity of the system needs to be guaranteed by the energy tank. We further propose a generic vector field decomposition strategy based on conservative stiffness, which effectively slows down the decay rate of energy in the energy tank and improves the stability margin of the control system. Finally, a series of simulations in various scenarios and experiments on planar and curved motion tasks demonstrate the validity of our theory and methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge