Generalizing Topological Graph Neural Networks with Paths

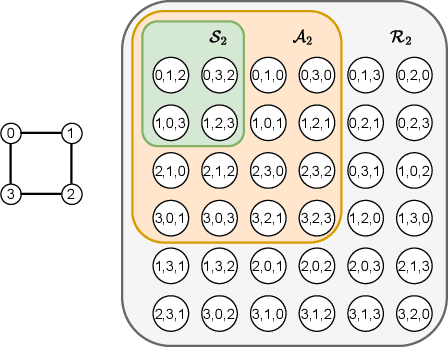
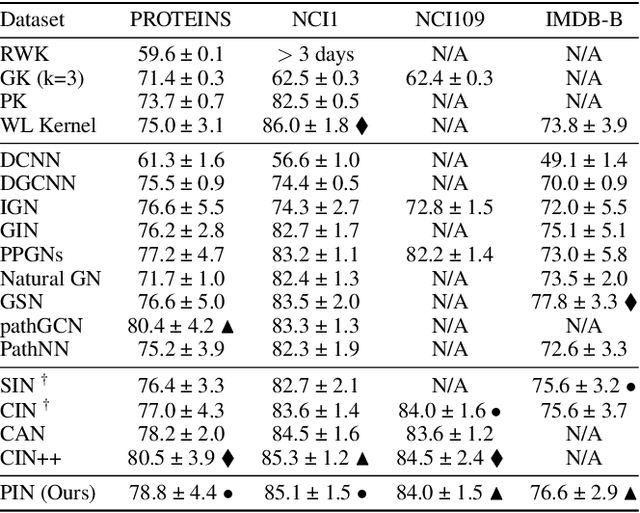
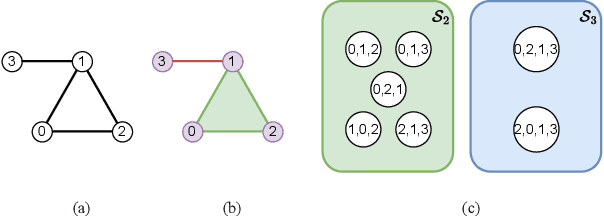
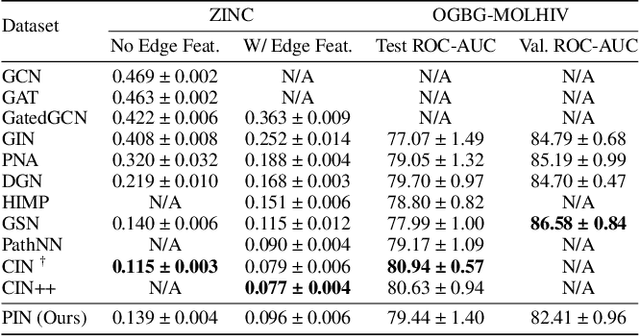
While Graph Neural Networks (GNNs) have made significant strides in diverse areas, they are hindered by a theoretical constraint known as the 1-Weisfeiler-Lehmann test. Even though latest advancements in higher-order GNNs can overcome this boundary, they typically center around certain graph components like cliques or cycles. However, our investigation goes a different route. We put emphasis on paths, which are inherent in every graph. We are able to construct a more general topological perspective and form a bridge to certain established theories about other topological domains. Interestingly, without any assumptions on graph sub-structures, our approach surpasses earlier techniques in this field, achieving state-of-the-art performance on several benchmarks.