Generalized Power Method for Generalized Orthogonal Procrustes Problem: Global Convergence and Optimization Landscape Analysis
Paper and Code
Jun 29, 2021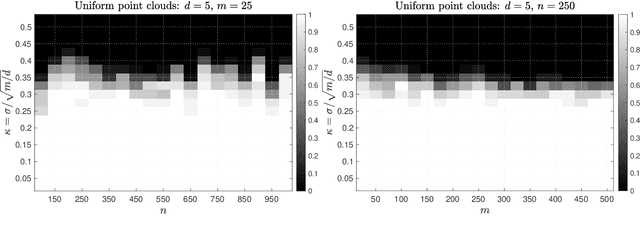

Given a set of multiple point clouds, how to find the rigid transformations (rotation, reflection, and shifting) such that these point clouds are well aligned? This problem, known as the generalized orthogonal Procrustes problem (GOPP), plays a fundamental role in several scientific disciplines including statistics, imaging science and computer vision. Despite its tremendous practical importance, it is still a challenging computational problem due to the inherent nonconvexity. In this paper, we study the semidefinite programming (SDP) relaxation of the generalized orthogonal Procrustes problems and prove that the tightness of the SDP relaxation holds, i.e., the SDP estimator exactly equals the least squares estimator, if the signal-to-noise ratio (SNR) is relatively large. We also prove that an efficient generalized power method with a proper initialization enjoys global linear convergence to the least squares estimator. In addition, we analyze the Burer-Monteiro factorization and show the corresponding optimization landscape is free of spurious local optima if the SNR is large. This explains why first-order Riemannian gradient methods with random initializations usually produce a satisfactory solution despite the nonconvexity. One highlight of our work is that the theoretical guarantees are purely algebraic and do not require any assumptions on the statistical property of the noise. Our results partially resolve one open problem posed in [Bandeira, Khoo, Singer, 2014] on the tightness of the SDP relaxation in solving the generalized orthogonal Procrustes problem. Numerical simulations are provided to complement our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge