Generalized Invariant Matching Property via LASSO
Paper and Code
Jan 14, 2023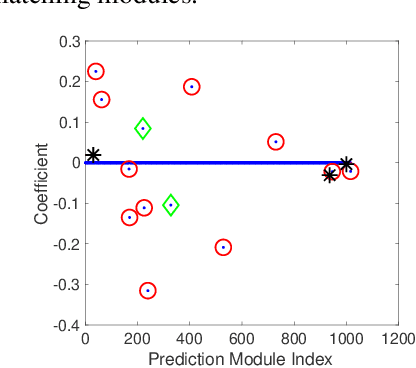
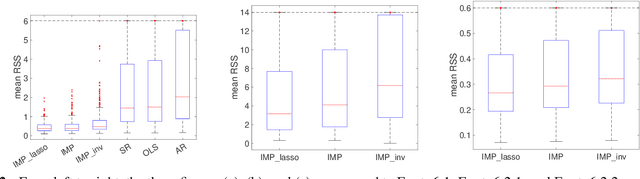
Learning under distribution shifts is a challenging task. One principled approach is to exploit the invariance principle via the structural causal models. However, the invariance principle is violated when the response is intervened, making it a difficult setting. In a recent work, the invariant matching property has been developed to shed light on this scenario and shows promising performance. In this work, we generalize the invariant matching property by formulating a high-dimensional problem with intrinsic sparsity. We propose a more robust and computation-efficient algorithm by leveraging a variant of Lasso, improving upon the existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge