Generalized Dantzig Selector: Application to the k-support norm
Paper and Code
Feb 02, 2015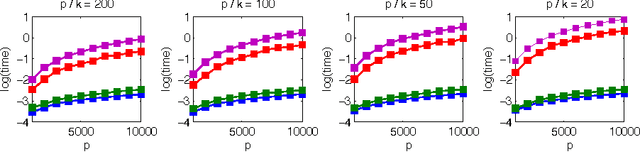
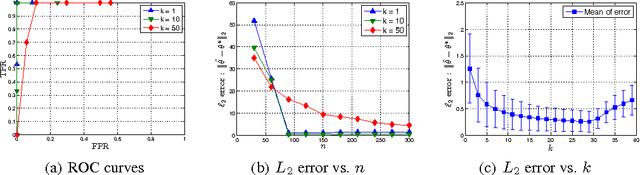
We propose a Generalized Dantzig Selector (GDS) for linear models, in which any norm encoding the parameter structure can be leveraged for estimation. We investigate both computational and statistical aspects of the GDS. Based on conjugate proximal operator, a flexible inexact ADMM framework is designed for solving GDS, and non-asymptotic high-probability bounds are established on the estimation error, which rely on Gaussian width of unit norm ball and suitable set encompassing estimation error. Further, we consider a non-trivial example of the GDS using $k$-support norm. We derive an efficient method to compute the proximal operator for $k$-support norm since existing methods are inapplicable in this setting. For statistical analysis, we provide upper bounds for the Gaussian widths needed in the GDS analysis, yielding the first statistical recovery guarantee for estimation with the $k$-support norm. The experimental results confirm our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge