Generalized Constraints as A New Mathematical Problem in Artificial Intelligence: A Review and Perspective
Paper and Code
Nov 12, 2020
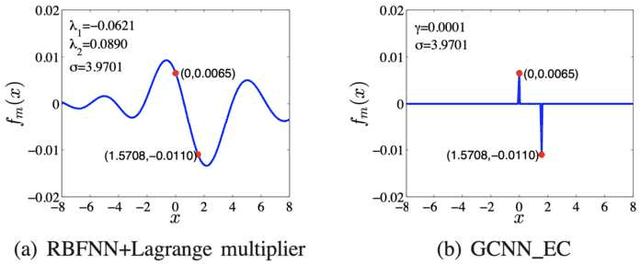

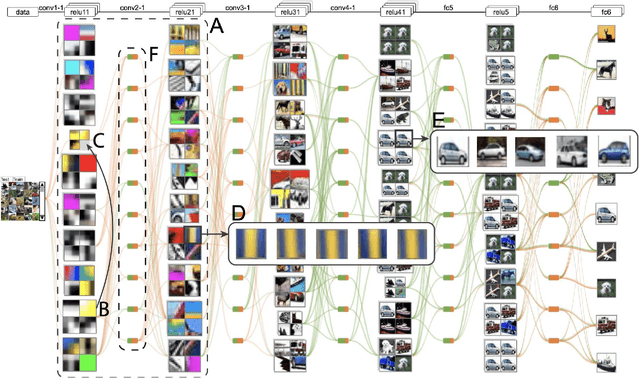
In this comprehensive review, we describe a new mathematical problem in artificial intelligence (AI) from a mathematical modeling perspective, following the philosophy stated by Rudolf E. Kalman that "Once you get the physics right, the rest is mathematics". The new problem is called "Generalized Constraints (GCs)", and we adopt GCs as a general term to describe any type of prior information in modelings. To understand better about GCs to be a general problem, we compare them with the conventional constraints (CCs) and list their extra challenges over CCs. In the construction of AI machines, we basically encounter more often GCs for modeling, rather than CCs with well-defined forms. Furthermore, we discuss the ultimate goals of AI and redefine transparent, interpretable, and explainable AI in terms of comprehension levels about machines. We review the studies in relation to the GC problems although most of them do not take the notion of GCs. We demonstrate that if AI machines are simplified by a coupling with both knowledge-driven submodel and data-driven submodel, GCs will play a critical role in a knowledge-driven submodel as well as in the coupling form between the two submodels. Examples are given to show that the studies in view of a generalized constraint problem will help us perceive and explore novel subjects in AI, or even in mathematics, such as generalized constraint learning (GCL).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge