Generalised learning of time-series: Ornstein-Uhlenbeck processes

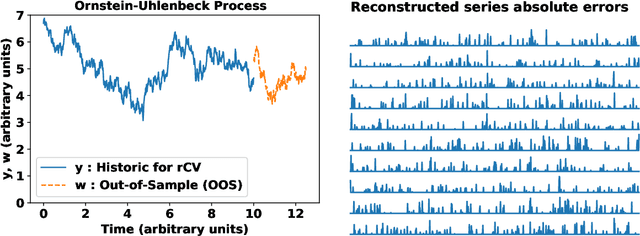
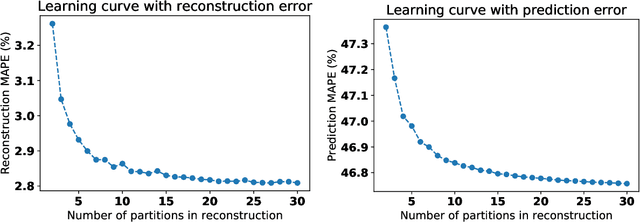
In machine learning, statistics, econometrics and statistical physics, $k$-fold cross-validation (CV) is used as a standard approach in quantifying the generalization performance of a statistical model. Applying this approach directly to time series models is avoided by practitioners due to intrinsic nature of serial correlations in the ordered data due to implications like absurdity of using future data to predict past and non-stationarity issues. In this work, we propose a technique called {\it reconstructive cross validation} ($rCV$) that avoids all these issues enabling generalized learning in time-series as a meta-algorithm. In $rCV$, data points in the test fold, randomly selected points from the time series, are first removed. Then, a secondary time series model or a technique is used in reconstructing the removed points from the test fold, i.e., imputation or smoothing. Thereafter, the primary model is build using new dataset coming from the secondary model or a technique. The performance of the primary model on the test set by computing the deviations from the originally removed and out-of-sample (OSS) data are evaluated simultaneously. This amounts to reconstruction and prediction errors. By this procedure serial correlations and data order is retained and $k$-fold cross-validation is reached generically. If reconstruction model uses a technique whereby the existing data points retained exactly, such as Gaussian process regression, the reconstruction itself will not result in information loss from non-reconstructed portion of the original data points. We have applied $rCV$ to estimate the general performance of the model build on simulated Ornstein-Uhlenbeck process. We have shown an approach to build a time-series learning curves utilizing $rCV$.