Gaussian Process Volatility Model
Paper and Code
Feb 13, 2014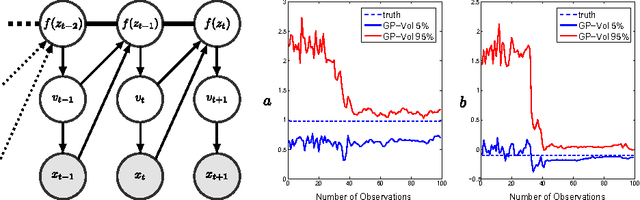
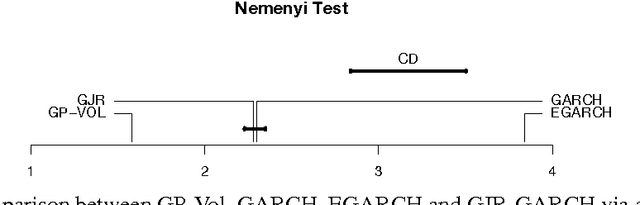
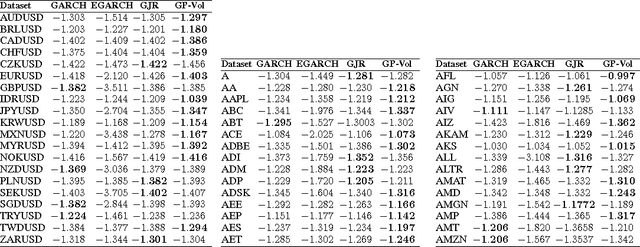
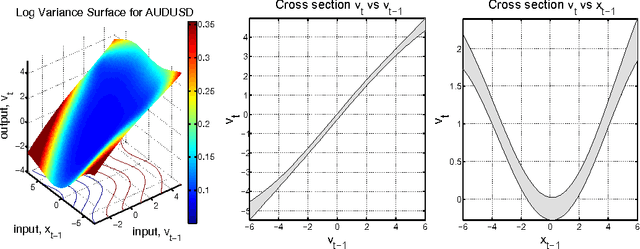
The accurate prediction of time-changing variances is an important task in the modeling of financial data. Standard econometric models are often limited as they assume rigid functional relationships for the variances. Moreover, function parameters are usually learned using maximum likelihood, which can lead to overfitting. To address these problems we introduce a novel model for time-changing variances using Gaussian Processes. A Gaussian Process (GP) defines a distribution over functions, which allows us to capture highly flexible functional relationships for the variances. In addition, we develop an online algorithm to perform inference. The algorithm has two main advantages. First, it takes a Bayesian approach, thereby avoiding overfitting. Second, it is much quicker than current offline inference procedures. Finally, our new model was evaluated on financial data and showed significant improvement in predictive performance over current standard models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge