Gaussian MRF Covariance Modeling for Efficient Black-Box Adversarial Attacks
Paper and Code
Oct 08, 2020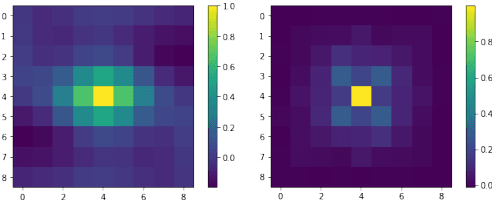
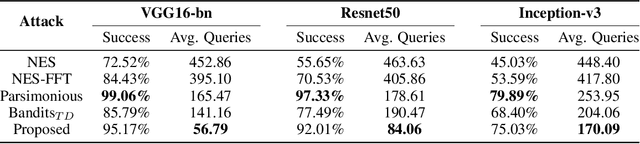
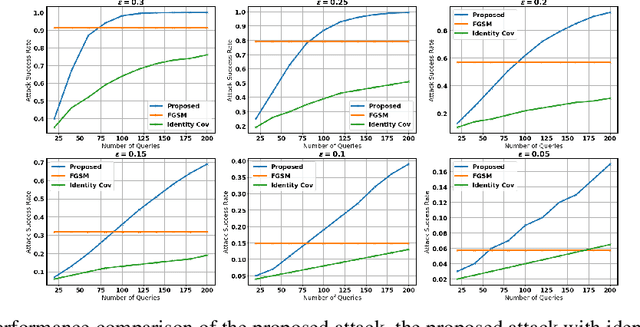
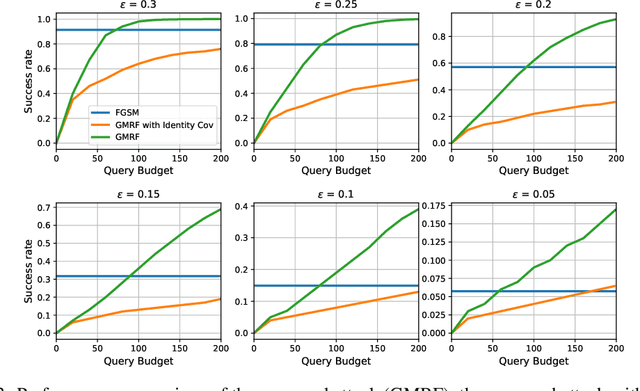
We study the problem of generating adversarial examples in a black-box setting, where we only have access to a zeroth order oracle, providing us with loss function evaluations. Although this setting has been investigated in previous work, most past approaches using zeroth order optimization implicitly assume that the gradients of the loss function with respect to the input images are \emph{unstructured}. In this work, we show that in fact substantial correlations exist within these gradients, and we propose to capture these correlations via a Gaussian Markov random field (GMRF). Given the intractability of the explicit covariance structure of the MRF, we show that the covariance structure can be efficiently represented using the Fast Fourier Transform (FFT), along with low-rank updates to perform exact posterior estimation under this model. We use this modeling technique to find fast one-step adversarial attacks, akin to a black-box version of the Fast Gradient Sign Method~(FGSM), and show that the method uses fewer queries and achieves higher attack success rates than the current state of the art. We also highlight the general applicability of this gradient modeling setup.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge