Gauss-Newton Dynamics for Neural Networks: A Riemannian Optimization Perspective
Paper and Code
Dec 19, 2024
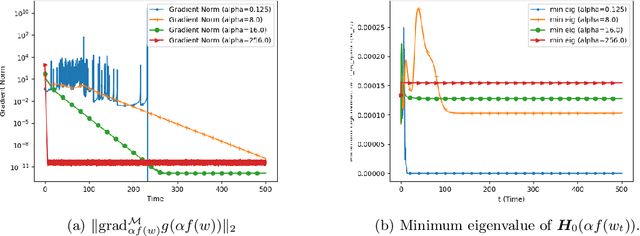
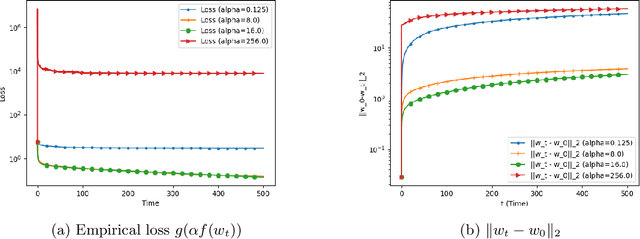
We analyze the convergence of Gauss-Newton dynamics for training neural networks with smooth activation functions. In the underparameterized regime, the Gauss-Newton gradient flow induces a Riemannian gradient flow on a low-dimensional, smooth, embedded submanifold of the Euclidean output space. Using tools from Riemannian optimization, we prove \emph{last-iterate} convergence of the Riemannian gradient flow to the optimal in-class predictor at an \emph{exponential rate} that is independent of the conditioning of the Gram matrix, \emph{without} requiring explicit regularization. We further characterize the critical impacts of the neural network scaling factor and the initialization on the convergence behavior. In the overparameterized regime, we show that the Levenberg-Marquardt dynamics with an appropriately chosen damping factor yields robustness to ill-conditioned kernels, analogous to the underparameterized regime. These findings demonstrate the potential of Gauss-Newton methods for efficiently optimizing neural networks, particularly in ill-conditioned problems where kernel and Gram matrices have small singular values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge