Game of Coding With an Unknown Adversary

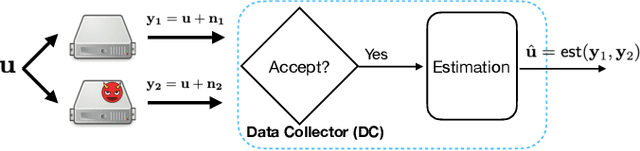
Motivated by emerging decentralized applications, the \emph{game of coding} framework has been recently introduced to address scenarios where the adversary's control over coded symbols surpasses the fundamental limits of traditional coding theory. Still, the reward mechanism available in decentralized systems, motivates the adversary to act rationally. While the decoder, as the data collector (DC), has an acceptance and rejection mechanism, followed by an estimation module, the adversary aims to maximize its utility, as an increasing function of (1) the chance of acceptance (to increase the reward), and (2) estimation error. On the other hand, the decoder also adjusts its acceptance rule to maximize its own utility, as (1) an increasing function of the chance of acceptance (to keep the system functional), (2) decreasing function of the estimation error. Prior works within this framework rely on the assumption that the game is complete, that is, both the DC and the adversary are fully aware of each other's utility functions. However, in practice, the decoder is often unaware of the utility of the adversary. To address this limitation, we develop an algorithm enabling the DC to commit to a strategy that achieves within the vicinity of the equilibrium, without knowledge of the adversary's utility function. Our approach builds on an observation that at the equilibrium, the relationship between the probability of acceptance and the mean squared error (MSE) follows a predetermined curve independent of the specific utility functions of the players. By exploiting this invariant relationship, the DC can iteratively refine its strategy based on observable parameters, converging to a near-optimal solution. We provide theoretical guarantees on sample complexity and accuracy of the proposed scheme.