Galerkin Neural Networks: A Framework for Approximating Variational Equations with Error Control
Paper and Code
May 28, 2021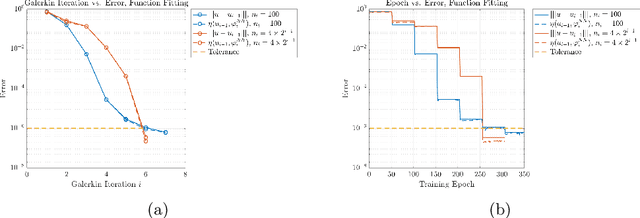
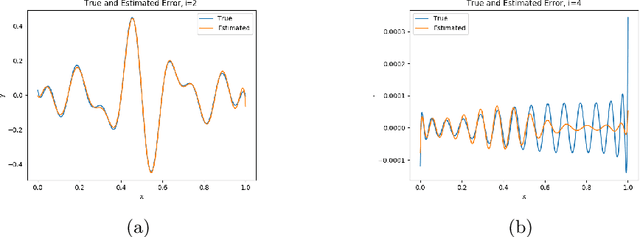
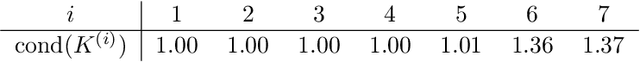
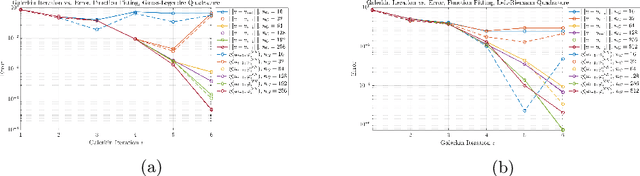
We present a new approach to using neural networks to approximate the solutions of variational equations, based on the adaptive construction of a sequence of finite-dimensional subspaces whose basis functions are realizations of a sequence of neural networks. The finite-dimensional subspaces are then used to define a standard Galerkin approximation of the variational equation. This approach enjoys a number of advantages, including: the sequential nature of the algorithm offers a systematic approach to enhancing the accuracy of a given approximation; the sequential enhancements provide a useful indicator for the error that can be used as a criterion for terminating the sequential updates; the basic approach is largely oblivious to the nature of the partial differential equation under consideration; and, some basic theoretical results are presented regarding the convergence (or otherwise) of the method which are used to formulate basic guidelines for applying the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge