Functional Currents : a new mathematical tool to model and analyse functional shapes
Paper and Code
Jun 15, 2012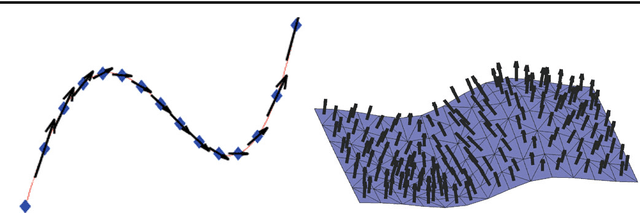
This paper introduces the concept of functional current as a mathematical framework to represent and treat functional shapes, i.e. sub-manifold supported signals. It is motivated by the growing occurrence, in medical imaging and computational anatomy, of what can be described as geometrico-functional data, that is a data structure that involves a deformable shape (roughly a finite dimensional sub manifold) together with a function defined on this shape taking value in another manifold. Indeed, if mathematical currents have already proved to be very efficient theoretically and numerically to model and process shapes as curves or surfaces, they are limited to the manipulation of purely geometrical objects. We show that the introduction of the concept of functional currents offers a genuine solution to the simultaneous processing of the geometric and signal information of any functional shape. We explain how functional currents can be equipped with a Hilbertian norm mixing geometrical and functional content of functional shapes nicely behaving under geometrical and functional perturbations and paving the way to various processing algorithms. We illustrate this potential on two problems: the redundancy reduction of functional shapes representations through matching pursuit schemes on functional currents and the simultaneous geometric and functional registration of functional shapes under diffeomorphic transport.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge