From Finite to Countable-Armed Bandits
Paper and Code
May 22, 2021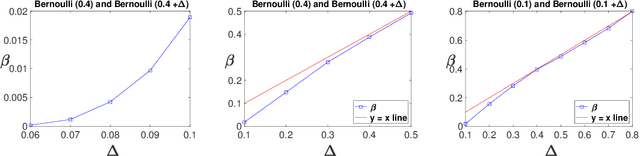
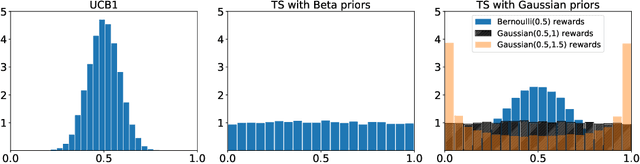
We consider a stochastic bandit problem with countably many arms that belong to a finite set of types, each characterized by a unique mean reward. In addition, there is a fixed distribution over types which sets the proportion of each type in the population of arms. The decision maker is oblivious to the type of any arm and to the aforementioned distribution over types, but perfectly knows the total number of types occurring in the population of arms. We propose a fully adaptive online learning algorithm that achieves O(log n) distribution-dependent expected cumulative regret after any number of plays n, and show that this order of regret is best possible. The analysis of our algorithm relies on newly discovered concentration and convergence properties of optimism-based policies like UCB in finite-armed bandit problems with "zero gap," which may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge