FriendlyCore: Practical Differentially Private Aggregation
Paper and Code
Oct 19, 2021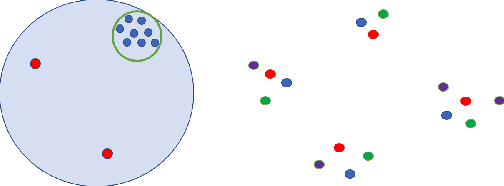
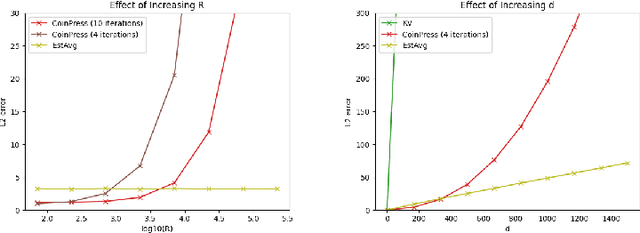
Differentially private algorithms for common metric aggregation tasks, such as clustering or averaging, often have limited practicality due to their complexity or a large number of data points that is required for accurate results. We propose a simple and practical tool $\mathsf{FriendlyCore}$ that takes a set of points ${\cal D}$ from an unrestricted (pseudo) metric space as input. When ${\cal D}$ has effective diameter $r$, $\mathsf{FriendlyCore}$ returns a "stable" subset ${\cal D}_G\subseteq {\cal D}$ that includes all points, except possibly few outliers, and is {\em certified} to have diameter $r$. $\mathsf{FriendlyCore}$ can be used to preprocess the input before privately aggregating it, potentially simplifying the aggregation or boosting its accuracy. Surprisingly, $\mathsf{FriendlyCore}$ is light-weight with no dependence on the dimension. We empirically demonstrate its advantages in boosting the accuracy of mean estimation, outperforming tailored methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge