Friction Variability in Planar Pushing Data: Anisotropic Friction and Data-collection Bias
Paper and Code
Jun 22, 2018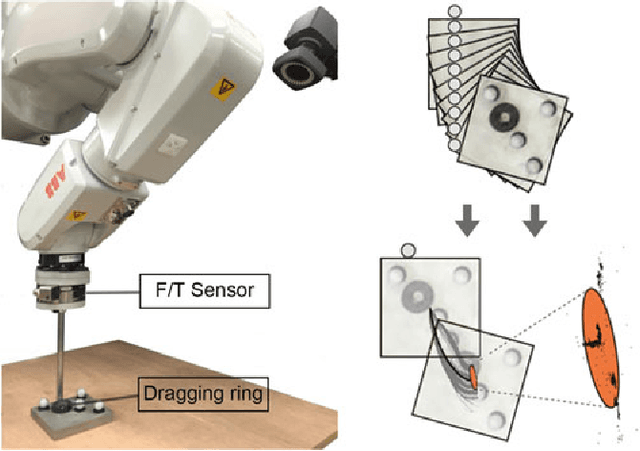
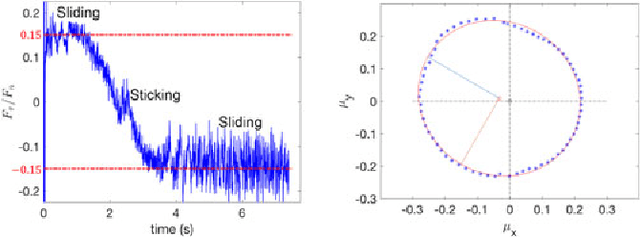
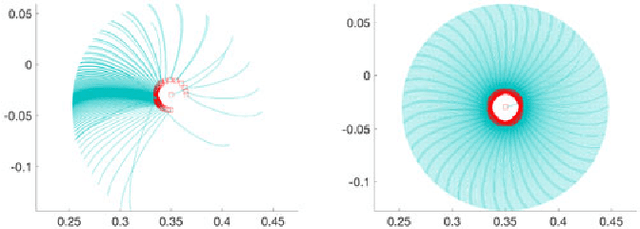
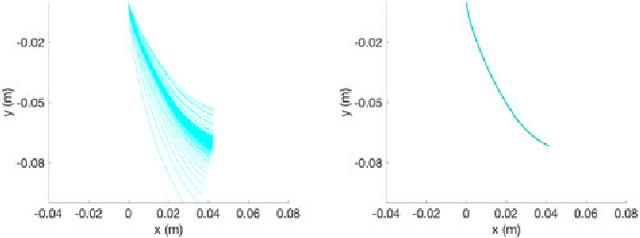
Friction plays a key role in manipulating objects. Most of what we do with our hands, and most of what robots do with their grippers, is based on the ability to control frictional forces. This paper aims to better understand the variability and predictability of planar friction. In particular, we focus on the analysis of a recent dataset on planar pushing by Yu et al. [1] devised to create a data-driven footprint of planar friction. We show in this paper how we can explain a significant fraction of the observed unconventional phenomena, e.g., stochasticity and multi-modality, by combining the effects of material non-homogeneity, anisotropy of friction and biases due to data collection dynamics, hinting that the variability is explainable but inevitable in practice. We introduce an anisotropic friction model and conduct simulation experiments comparing with more standard isotropic friction models. The anisotropic friction between object and supporting surface results in convergence of initial condition during the automated data collection. Numerical results confirm that the anisotropic friction model explains the bias in the dataset and the apparent stochasticity in the outcome of a push. The fact that the data collection process itself can originate biases in the collected datasets, resulting in deterioration of trained models, calls attention to the data collection dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge