Framework for Designing Filters of Spectral Graph Convolutional Neural Networks in the Context of Regularization Theory
Paper and Code
Sep 29, 2020
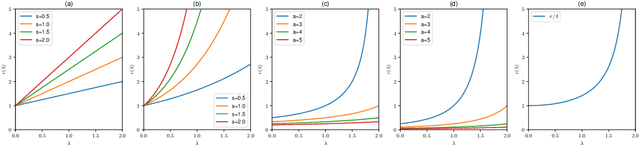

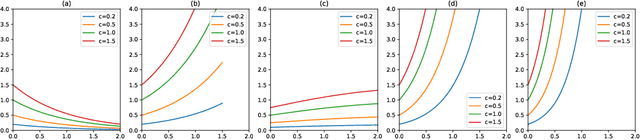
Graph convolutional neural networks (GCNNs) have been widely used in graph learning. It has been observed that the smoothness functional on graphs can be defined in terms of the graph Laplacian. This fact points out in the direction of using Laplacian in deriving regularization operators on graphs and its consequent use with spectral GCNN filter designs. In this work, we explore the regularization properties of graph Laplacian and proposed a generalized framework for regularized filter designs in spectral GCNNs. We found that the filters used in many state-of-the-art GCNNs can be derived as a special case of the framework we developed. We designed new filters that are associated with well-defined regularization behavior and tested their performance on semi-supervised node classification tasks. Their performance was found to be superior to that of the other state-of-the-art techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge