Fourier Series Guided Design of Quantum Convolutional Neural Networks for Enhanced Time Series Forecasting
Paper and Code
Apr 25, 2024
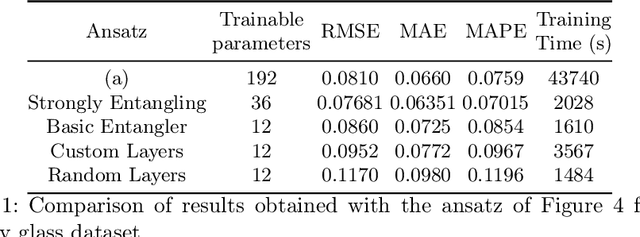
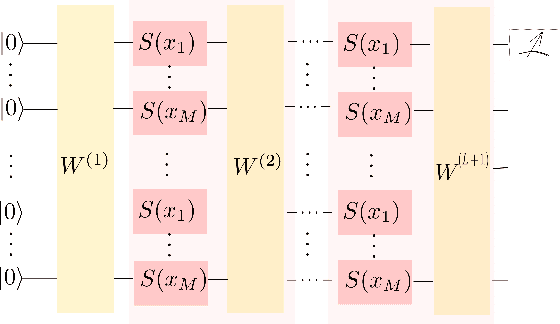
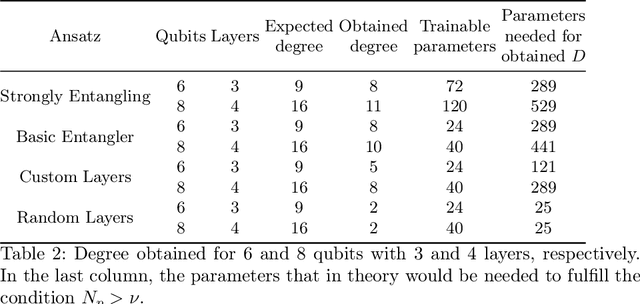
In this study, we apply 1D quantum convolution to address the task of time series forecasting. By encoding multiple points into the quantum circuit to predict subsequent data, each point becomes a feature, transforming the problem into a multidimensional one. Building on theoretical foundations from prior research, which demonstrated that Variational Quantum Circuits (VQCs) can be expressed as multidimensional Fourier series, we explore the capabilities of different architectures and ansatz. This analysis considers the concepts of circuit expressibility and the presence of barren plateaus. Analyzing the problem within the framework of the Fourier series enabled the design of an architecture that incorporates data reuploading, resulting in enhanced performance. Rather than a strict requirement for the number of free parameters to exceed the degrees of freedom of the Fourier series, our findings suggest that even a limited number of parameters can produce Fourier functions of higher degrees. This highlights the remarkable expressive power of quantum circuits. This observation is also significant in reducing training times. The ansatz with greater expressibility and number of non-zero Fourier coefficients consistently delivers favorable results across different scenarios, with performance metrics improving as the number of qubits increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge