Foundation Posteriors for Approximate Probabilistic Inference

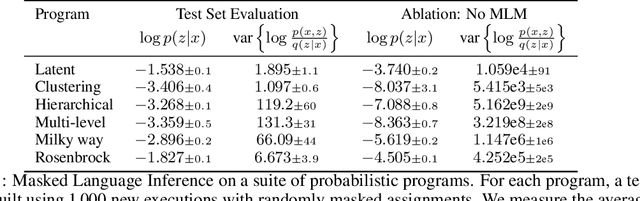
Probabilistic programs provide an expressive representation language for generative models. Given a probabilistic program, we are interested in the task of posterior inference: estimating a latent variable given a set of observed variables. Existing techniques for inference in probabilistic programs often require choosing many hyper-parameters, are computationally expensive, and/or only work for restricted classes of programs. Here we formulate inference as masked language modeling: given a program, we generate a supervised dataset of variables and assignments, and randomly mask a subset of the assignments. We then train a neural network to unmask the random values, defining an approximate posterior distribution. By optimizing a single neural network across a range of programs we amortize the cost of training, yielding a ``foundation'' posterior able to do zero-shot inference for new programs. The foundation posterior can also be fine-tuned for a particular program and dataset by optimizing a variational inference objective. We show the efficacy of the approach, zero-shot and fine-tuned, on a benchmark of STAN programs.