floZ: Evidence estimation from posterior samples with normalizing flows

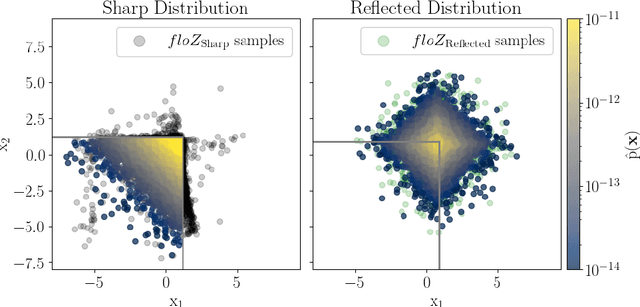
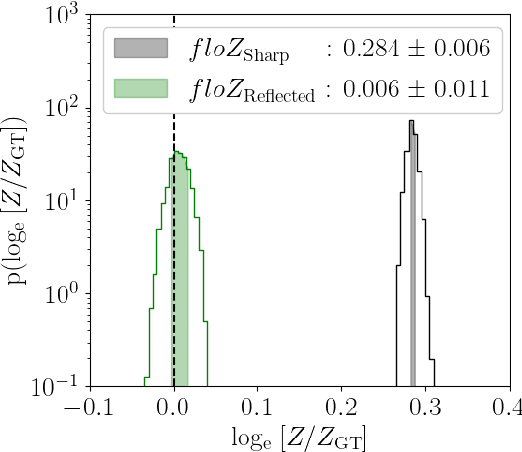
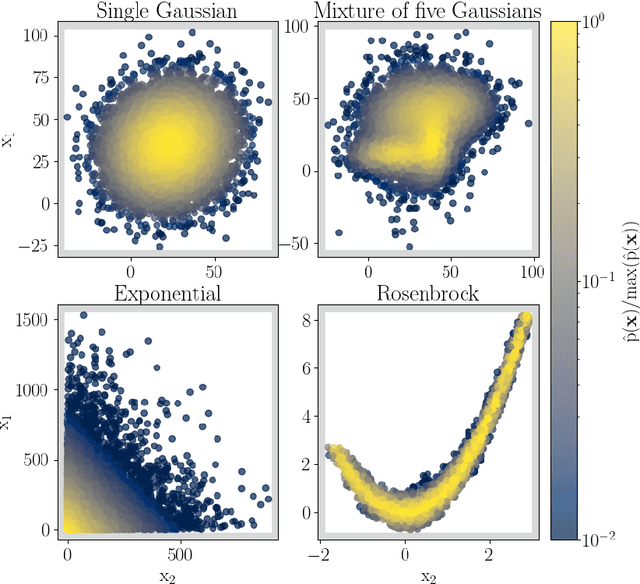
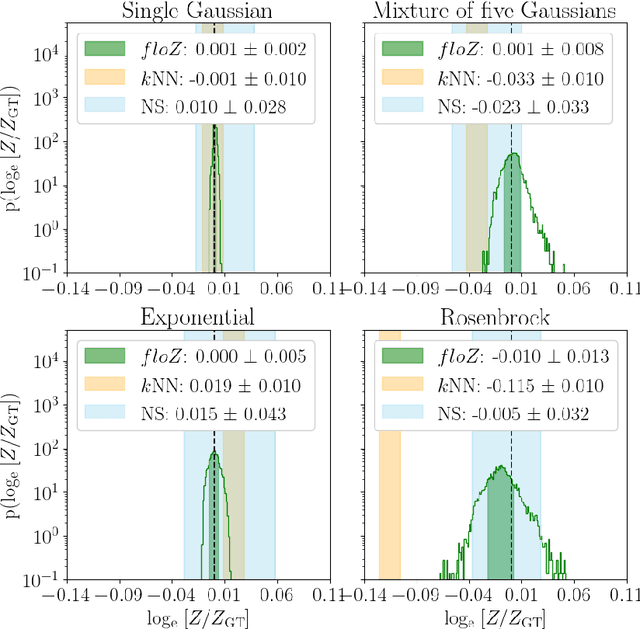
We propose a novel method (floZ), based on normalizing flows, for estimating the Bayesian evidence (and its numerical uncertainty) from a set of samples drawn from the unnormalized posterior distribution. We validate it on distributions whose evidence is known analytically, up to 15 parameter space dimensions, and compare with two state-of-the-art techniques for estimating the evidence: nested sampling (which computes the evidence as its main target) and a k-nearest-neighbors technique that produces evidence estimates from posterior samples. Provided representative samples from the target posterior are available, our method is more robust to posterior distributions with sharp features, especially in higher dimensions. It has wide applicability, e.g., to estimate the evidence from variational inference, Markov-chain Monte Carlo samples, or any other method that delivers samples from the unnormalized posterior density.