Flat Metric Minimization with Applications in Generative Modeling
Paper and Code
May 12, 2019
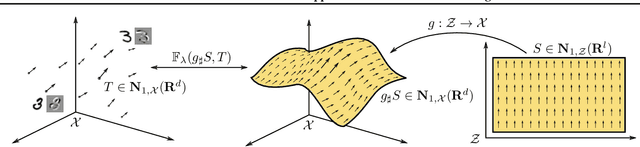
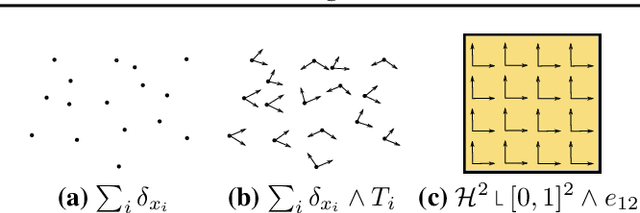
We take the novel perspective to view data not as a probability distribution but rather as a current. Primarily studied in the field of geometric measure theory, $k$-currents are continuous linear functionals acting on compactly supported smooth differential forms and can be understood as a generalized notion of oriented $k$-dimensional manifold. By moving from distributions (which are $0$-currents) to $k$-currents, we can explicitly orient the data by attaching a $k$-dimensional tangent plane to each sample point. Based on the flat metric which is a fundamental distance between currents, we derive FlatGAN, a formulation in the spirit of generative adversarial networks but generalized to $k$-currents. In our theoretical contribution we prove that the flat metric between a parametrized current and a reference current is Lipschitz continuous in the parameters. In experiments, we show that the proposed shift to $k>0$ leads to interpretable and disentangled latent representations which behave equivariantly to the specified oriented tangent planes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge