Finite-time disturbance reconstruction and robust fractional-order controller design for hybrid port-Hamiltonian dynamics of biped robots
Paper and Code
Jan 13, 2021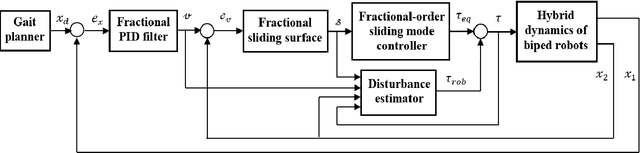

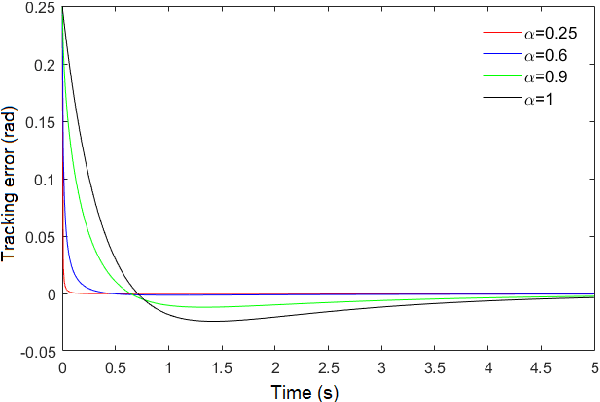

In this paper, disturbance reconstruction and robust trajectory tracking control of biped robots with hybrid dynamics in the port-Hamiltonian form is investigated. A new type of Hamiltonian function is introduced, which ensures the finite-time stability of the closed-loop system. The proposed control system consists of two loops: an inner and an outer loop. A fractional proportional-integral-derivative filter is used to achieve finite-time convergence for position tracking errors at the outer loop. A fractional-order sliding mode controller acts as a centralized controller at the inner-loop, ensuring the finite-time stability of the velocity tracking error. In this loop, the undesired effects of unknown external disturbance and parameter uncertainties are compensated using estimators. Two disturbance estimators are envisioned. The former is designed using fractional calculus. The latter is an adaptive estimator, and it is constructed using the general dynamic of biped robots. Stability analysis shows that the closed-loop system is finite-time stable in both contact-less and impact phases. Simulation studies on two types of biped robots (i.e., two-link walker and RABBIT biped robot) demonstrate the proposed controller's tracking performance and disturbance rejection capability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge