Fighting the curse of dimensionality: A machine learning approach to finding global optima

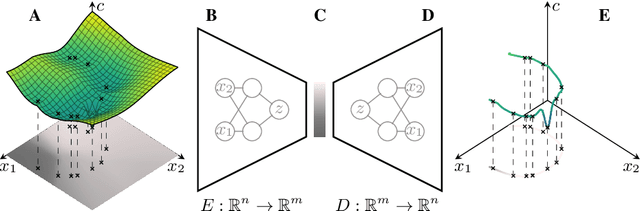
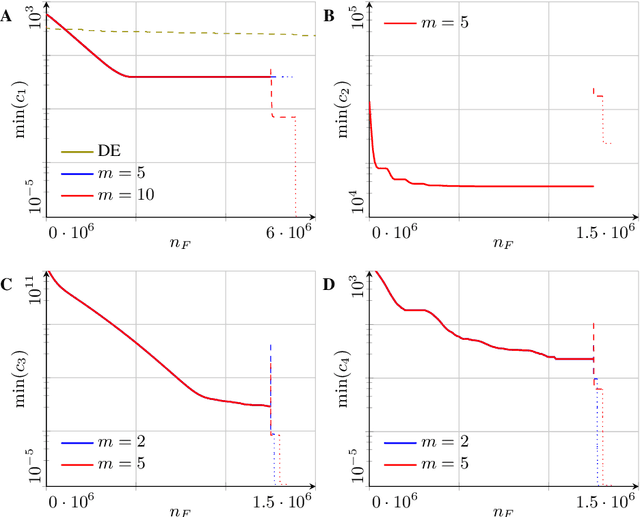
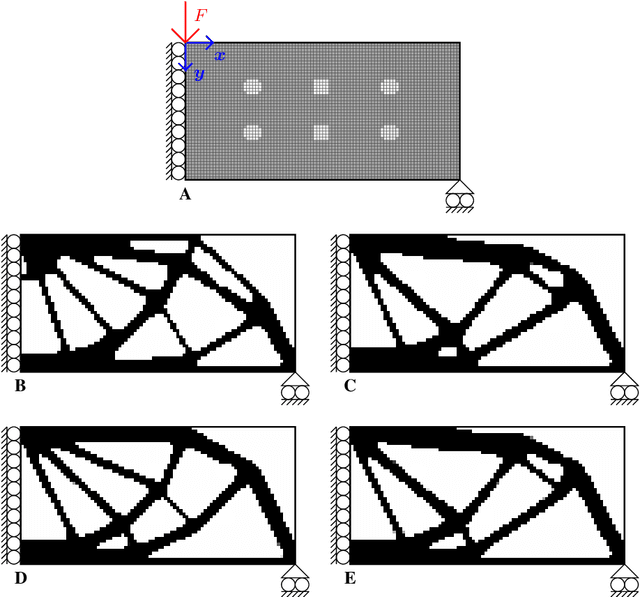
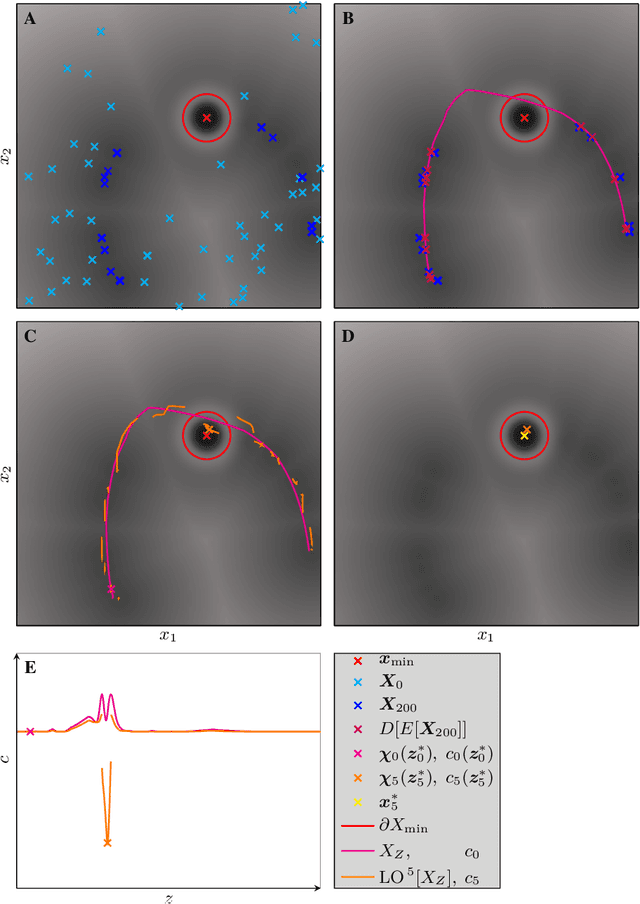
Finding global optima in high-dimensional optimization problems is extremely challenging since the number of function evaluations required to sufficiently explore the design space increases exponentially with its dimensionality. Furthermore, non-convex cost functions render local gradient-based search techniques ineffective. To overcome these difficulties, here we demonstrate the use of machine learning to find global minima, whereby autoencoders are used to drastically reduce the search space dimensionality, and optima are found by surveying the lower-dimensional latent spaces. The methodology is tested on benchmark functions and on a structural optimization problem, where we show that by exploiting the behavior of certain cost functions we either obtain the global optimum at best or obtain superior results at worst when compared to established optimization procedures.