FeO2: Federated Learning with Opt-Out Differential Privacy

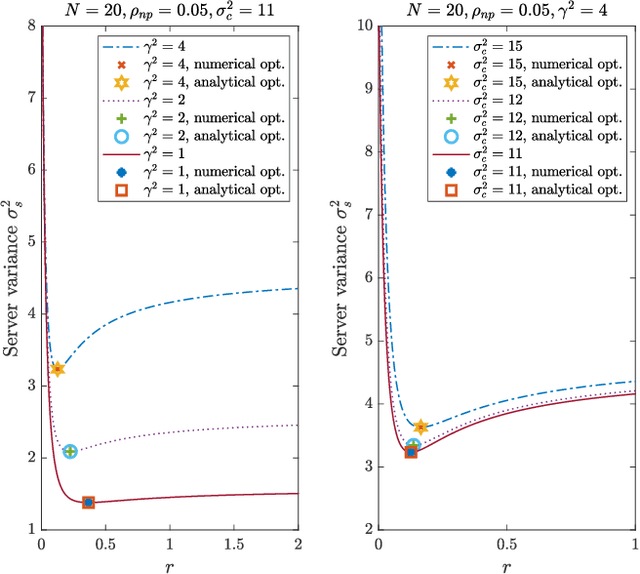
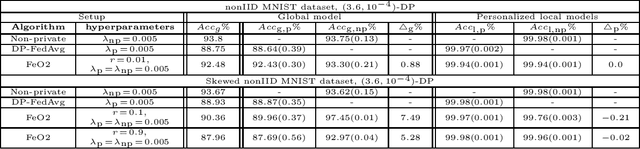
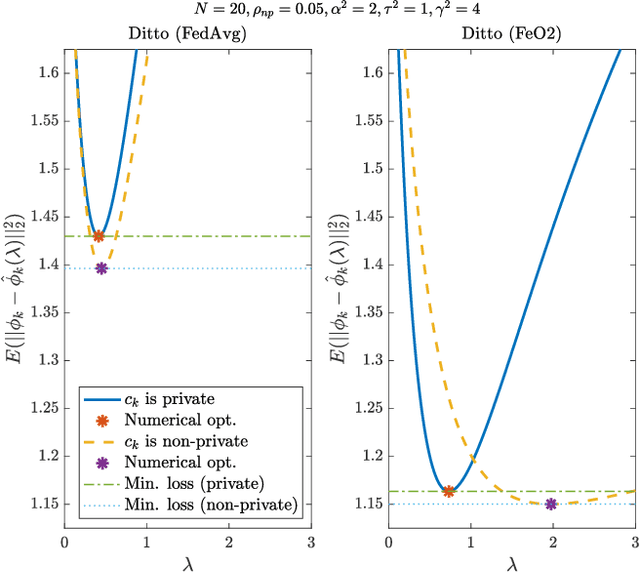
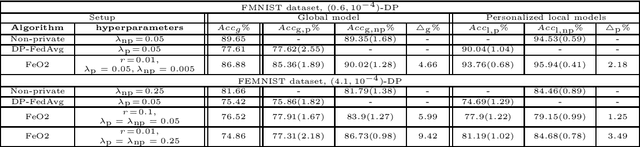
Federated learning (FL) is an emerging privacy-preserving paradigm, where a global model is trained at a central server while keeping client data local. However, FL can still indirectly leak private client information through model updates during training. Differential privacy (DP) can be employed to provide privacy guarantees within FL, typically at the cost of degraded final trained model. In this work, we consider a heterogeneous DP setup where clients are considered private by default, but some might choose to opt out of DP. We propose a new algorithm for federated learning with opt-out DP, referred to as \emph{FeO2}, along with a discussion on its advantages compared to the baselines of private and personalized FL algorithms. We prove that the server-side and client-side procedures in \emph{FeO2} are optimal for a simplified linear problem. We also analyze the incentive for opting out of DP in terms of performance gain. Through numerical experiments, we show that \emph{FeO2} provides up to $9.27\%$ performance gain in the global model compared to the baseline DP FL for the considered datasets. Additionally, we show a gap in the average performance of personalized models between non-private and private clients of up to $3.49\%$, empirically illustrating an incentive for clients to opt out.