Feasible Wrench Set Computation for Legged Robots
Paper and Code
Feb 03, 2022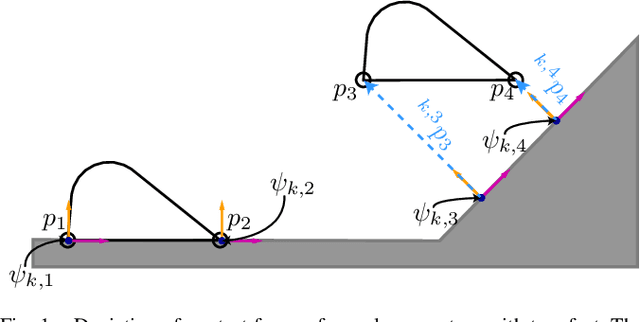


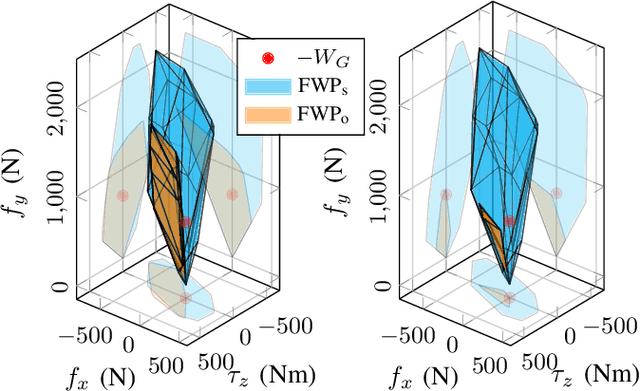
During locomotion, legged robots interact with the ground by sequentially establishing and breaking contact. The interaction wrenches that arise from contact are used to steer the robot's Center of Mass (CoM) and reject perturbations that make the system deviate from the desired trajectory and often make them fall. The feasibility of a given control target (desired CoM wrench or acceleration) is conditioned by the contact point distribution, ground friction, and actuation limits. In this work, we develop an algorithm to compute the set of feasible wrenches that a legged robot can exert on its CoM through contact. The presented method can be used with any amount of non-coplanar contacts and takes into account actuation limits and limitations based on an inelastic contact model with Coulomb friction. This is exemplified with a planar biped model standing with the feet at different heights. Exploiting assumptions from the contact model, we explain how to compute the set of wrenches that are feasible on the CoM when the contacts remain in position as well as the ones that are feasible when some of the contacts are broken. Therefore, this algorithm can be used to assess whether a switch in contact configuration is feasible while achieving a given control task. Furthermore, the method can be used to identify the directions in which the system is not actuated (i.e. a wrench cannot be exerted in those directions). We show how having a joint be actuated or passive can change the non-actuated wrench directions of a robot at a given pose using a spatial model of a lower-extremity exoskeleton. Therefore, this algorithm is also a useful tool for the design phase of the system. This work presents a useful tool for the control and design of legged systems that extends on the current state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge