Fast solver for J2-perturbed Lambert problem using deep neural network
Paper and Code
Jan 09, 2022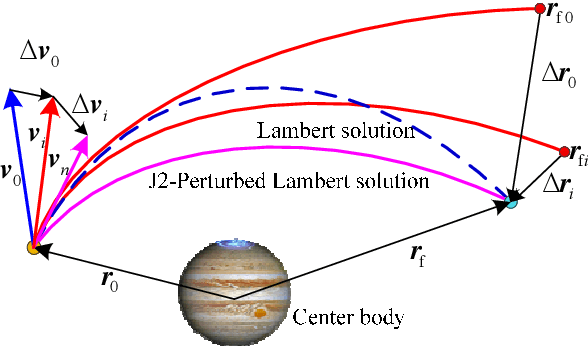
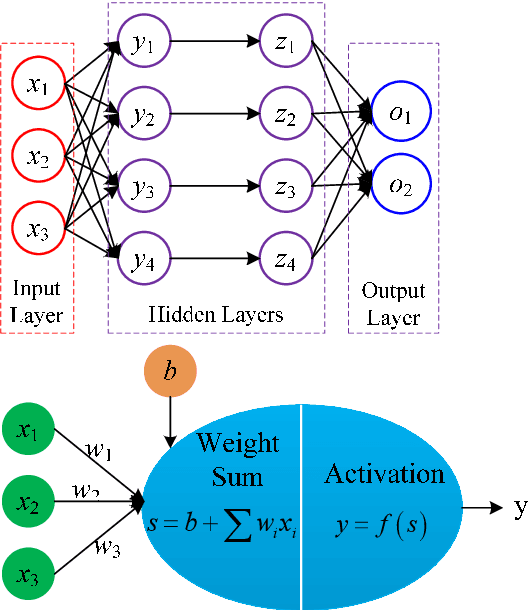

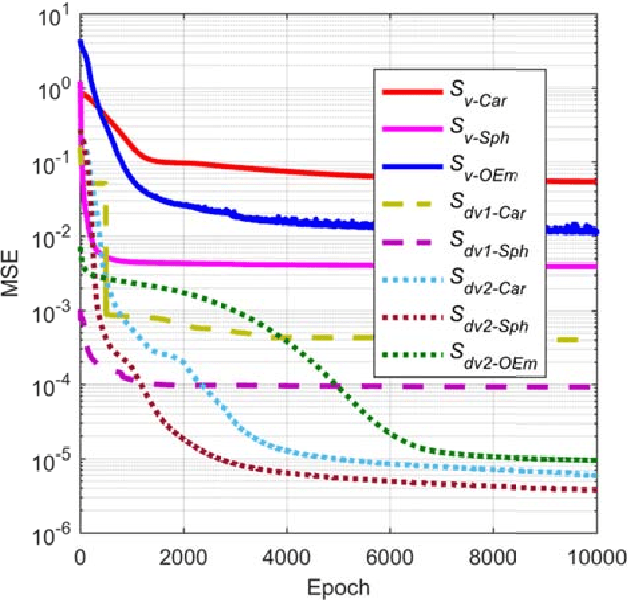
This paper presents a novel and fast solver for the J2-perturbed Lambert problem. The solver consists of an intelligent initial guess generator combined with a differential correction procedure. The intelligent initial guess generator is a deep neural network that is trained to correct the initial velocity vector coming from the solution of the unperturbed Lambert problem. The differential correction module takes the initial guess and uses a forward shooting procedure to further update the initial velocity and exactly meet the terminal conditions. Eight sample forms are analyzed and compared to find the optimum form to train the neural network on the J2-perturbed Lambert problem. The accuracy and performance of this novel approach will be demonstrated on a representative test case: the solution of a multi-revolution J2-perturbed Lambert problem in the Jupiter system. We will compare the performance of the proposed approach against a classical standard shooting method and a homotopy-based perturbed Lambert algorithm. It will be shown that, for a comparable level of accuracy, the proposed method is significantly faster than the other two.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge