Fast Moving Natural Evolution Strategy for High-Dimensional Problems
Paper and Code
Jan 27, 2022
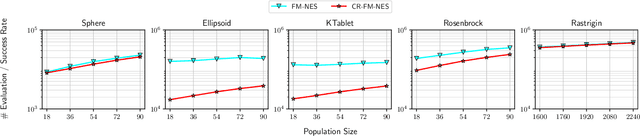

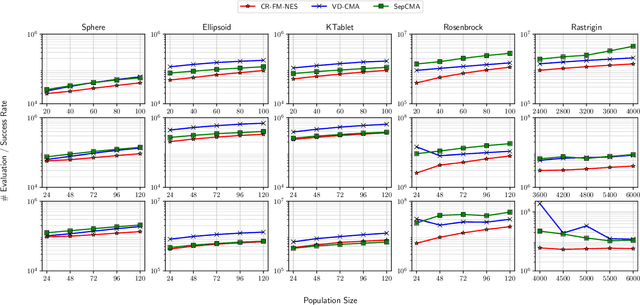
In this work, we propose a new variant of natural evolution strategies (NES) for high-dimensional black-box optimization problems. The proposed method, CR-FM-NES, extends a recently proposed state-of-the-art NES, Fast Moving Natural Evolution Strategy (FM-NES), in order to be applicable in high-dimensional problems. CR-FM-NES builds on an idea using a restricted representation of a covariance matrix instead of using a full covariance matrix, while inheriting an efficiency of FM-NES. The restricted representation of the covariance matrix enables CR-FM-NES to update parameters of a multivariate normal distribution in linear time and space complexity, which can be applied to high-dimensional problems. Our experimental results reveal that CR-FM-NES does not lose the efficiency of FM-NES, and on the contrary, CR-FM-NES has achieved significant speedup compared to FM-NES on some benchmark problems. Furthermore, our numerical experiments using 200, 600, and 1000-dimensional benchmark problems demonstrate that CR-FM-NES is effective over scalable baseline methods, VD-CMA and Sep-CMA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge