Fast Latent Factor Analysis via a Fuzzy PID-Incorporated Stochastic Gradient Descent Algorithm
Paper and Code
Mar 07, 2023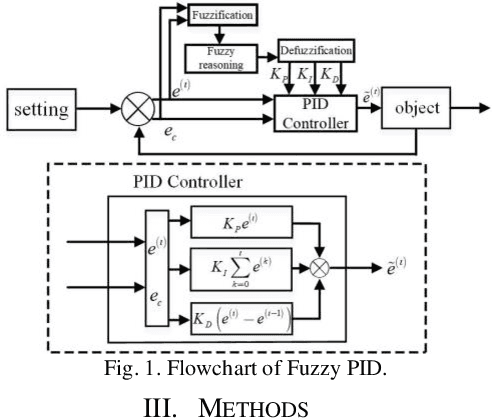

A high-dimensional and incomplete (HDI) matrix can describe the complex interactions among numerous nodes in various big data-related applications. A stochastic gradient descent (SGD)-based latent factor analysis (LFA) model is remarkably effective in extracting valuable information from an HDI matrix. However, such a model commonly encounters the problem of slow convergence because a standard SGD algorithm learns a latent factor relying on the stochastic gradient of current instance error only without considering past update information. To address this critical issue, this paper innovatively proposes a Fuzzy PID-incorporated SGD (FPS) algorithm with two-fold ideas: 1) rebuilding the instance learning error by considering the past update information in an efficient way following the principle of PID, and 2) implementing hyper-parameters and gain parameters adaptation following the fuzzy rules. With it, an FPS-incorporated LFA model is further achieved for fast processing an HDI matrix. Empirical studies on six HDI datasets demonstrate that the proposed FPS-incorporated LFA model significantly outperforms the state-of-the-art LFA models in terms of computational efficiency for predicting the missing data of an HDI matrix with competitive accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge