Fast Convex Quadratic Optimization Solvers with Adaptive Sketching-based Preconditioners
Paper and Code
Apr 29, 2021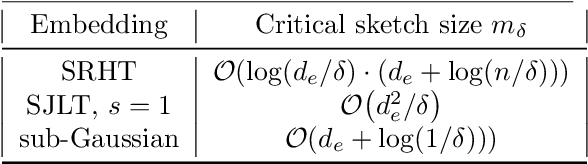



We consider least-squares problems with quadratic regularization and propose novel sketching-based iterative methods with an adaptive sketch size. The sketch size can be as small as the effective dimension of the data matrix to guarantee linear convergence. However, a major difficulty in choosing the sketch size in terms of the effective dimension lies in the fact that the latter is usually unknown in practice. Current sketching-based solvers for regularized least-squares fall short on addressing this issue. Our main contribution is to propose adaptive versions of standard sketching-based iterative solvers, namely, the iterative Hessian sketch and the preconditioned conjugate gradient method, that do not require a priori estimation of the effective dimension. We propose an adaptive mechanism to control the sketch size according to the progress made in each step of the iterative solver. If enough progress is not made, the sketch size increases to improve the convergence rate. We prove that the adaptive sketch size scales at most in terms of the effective dimension, and that our adaptive methods are guaranteed to converge linearly. Consequently, our adaptive methods improve the state-of-the-art complexity for solving dense, ill-conditioned least-squares problems. Importantly, we illustrate numerically on several synthetic and real datasets that our method is extremely efficient and is often significantly faster than standard least-squares solvers such as a direct factorization based solver, the conjugate gradient method and its preconditioned variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge