Fast Attributed Graph Embedding via Density of States
Paper and Code
Oct 11, 2021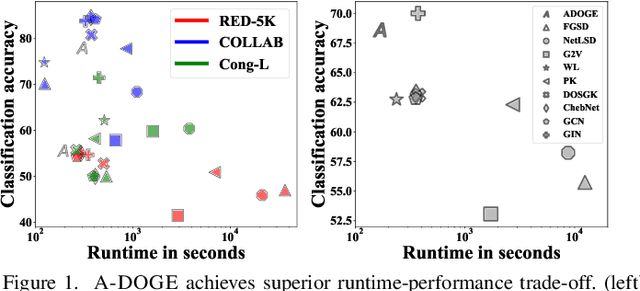
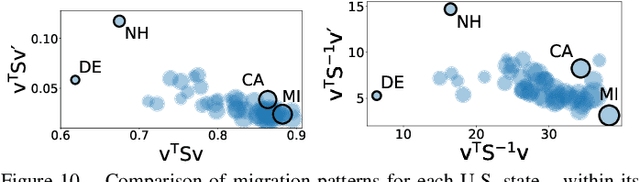
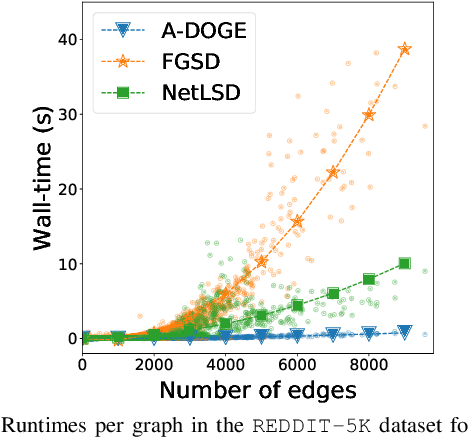
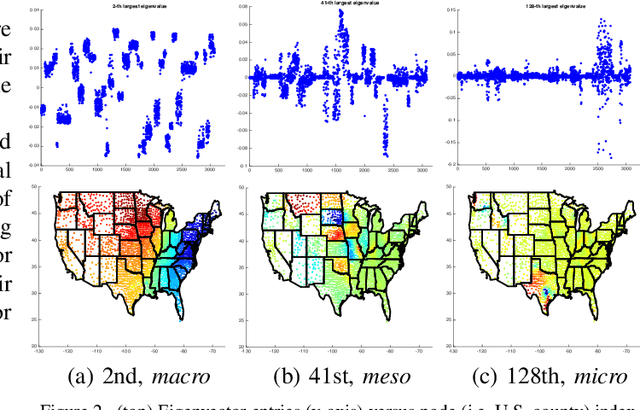
Given a node-attributed graph, how can we efficiently represent it with few numerical features that expressively reflect its topology and attribute information? We propose A-DOGE, for Attributed DOS-based Graph Embedding, based on density of states (DOS, a.k.a. spectral density) to tackle this problem. A-DOGE is designed to fulfill a long desiderata of desirable characteristics. Most notably, it capitalizes on efficient approximation algorithms for DOS, that we extend to blend in node labels and attributes for the first time, making it fast and scalable for large attributed graphs and graph databases. Being based on the entire eigenspectrum of a graph, A-DOGE can capture structural and attribute properties at multiple ("glocal") scales. Moreover, it is unsupervised (i.e. agnostic to any specific objective) and lends itself to various interpretations, which makes it is suitable for exploratory graph mining tasks. Finally, it processes each graph independent of others, making it amenable for streaming settings as well as parallelization. Through extensive experiments, we show the efficacy and efficiency of A-DOGE on exploratory graph analysis and graph classification tasks, where it significantly outperforms unsupervised baselines and achieves competitive performance with modern supervised GNNs, while achieving the best trade-off between accuracy and runtime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge