Extension of Wirtinger Calculus in RKH Spaces and the Complex Kernel LMS
Paper and Code
May 25, 2010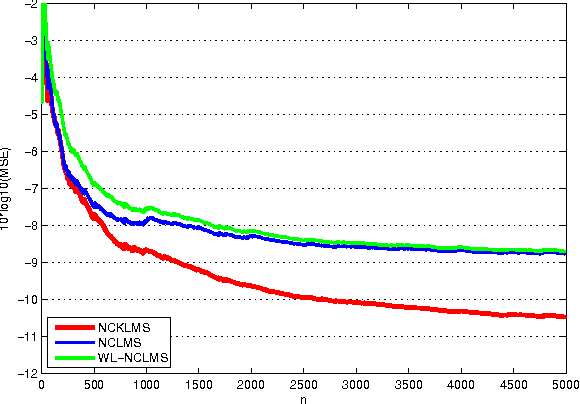
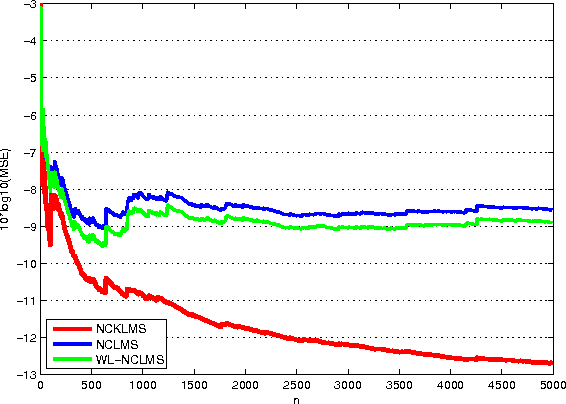
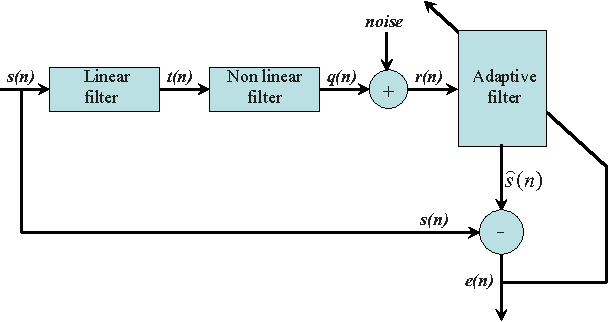
Over the last decade, kernel methods for nonlinear processing have successfully been used in the machine learning community. However, so far, the emphasis has been on batch techniques. It is only recently, that online adaptive techniques have been considered in the context of signal processing tasks. To the best of our knowledge, no kernel-based strategy has been developed, so far, that is able to deal with complex valued signals. In this paper, we take advantage of a technique called complexification of real RKHSs to attack this problem. In order to derive gradients and subgradients of operators that need to be defined on the associated complex RKHSs, we employ the powerful tool ofWirtinger's Calculus, which has recently attracted much attention in the signal processing community. Writinger's calculus simplifies computations and offers an elegant tool for treating complex signals. To this end, in this paper, the notion of Writinger's calculus is extended, for the first time, to include complex RKHSs and use it to derive the Complex Kernel Least-Mean-Square (CKLMS) algorithm. Experiments verify that the CKLMS can be used to derive nonlinear stable algorithms, which offer significant performance improvements over the traditional complex LMS orWidely Linear complex LMS (WL-LMS) algorithms, when dealing with nonlinearities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge