Extending the kinematic theory of rapid movements with new primitives
Paper and Code
Jan 29, 2024
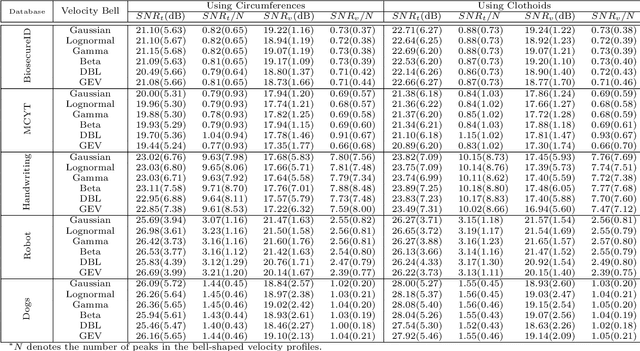
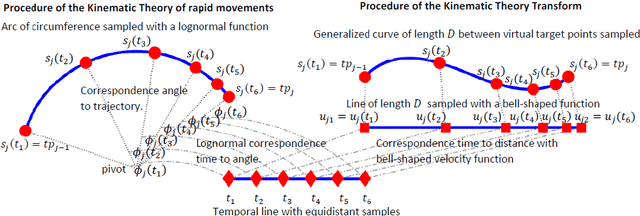

The Kinematic Theory of rapid movements, and its associated Sigma-Lognormal, model 2D spatiotemporal trajectories. It is constructed mainly as a temporal overlap of curves between virtual target points. Specifically, it uses an arc and a lognormal as primitives for the representation of the trajectory and velocity, respectively. This paper proposes developing this model, in what we call the Kinematic Theory Transform, which establishes a mathematical framework that allows further primitives to be used. Mainly, we evaluate Euler curves to link virtual target points and Gaussian, Beta, Gamma, Double-bounded lognormal, and Generalized Extreme Value functions to model the bell-shaped velocity profile. Using these primitives, we report reconstruction results with spatiotemporal trajectories executed by human beings, animals, and anthropomorphic robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge