Exponentially-Modified Gaussian Mixture Model: Applications in Spectroscopy

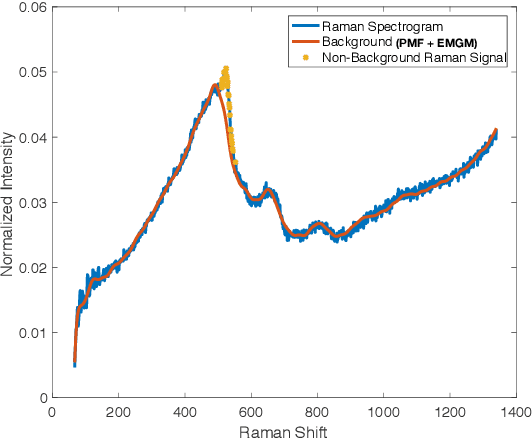
We propose a novel exponentially-modified Gaussian (EMG) mixture residual model. The EMG mixture is well suited to model residuals that are contaminated by a distribution with positive support. This is in contrast to commonly used robust residual models, like the Huber loss or $\ell_1$, which assume a symmetric contaminating distribution and are otherwise asymptotically biased. We propose an expectation-maximization algorithm to optimize an arbitrary model with respect to the EMG mixture. We apply the approach to linear regression and probabilistic matrix factorization (PMF). We compare against other residual models, including quantile regression. Our numerical experiments demonstrate the strengths of the EMG mixture on both tasks. The PMF model arises from considering spectroscopic data. In particular, we demonstrate the effectiveness of PMF in conjunction with the EMG mixture model on synthetic data and two real-world applications: X-ray diffraction and Raman spectroscopy. We show how our approach is effective in inferring background signals and systematic errors in data arising from these experimental settings, dramatically outperforming existing approaches and revealing the data's physically meaningful components.