Exponentially Consistent Nonparametric Clustering of Data Streams
Paper and Code
Nov 21, 2024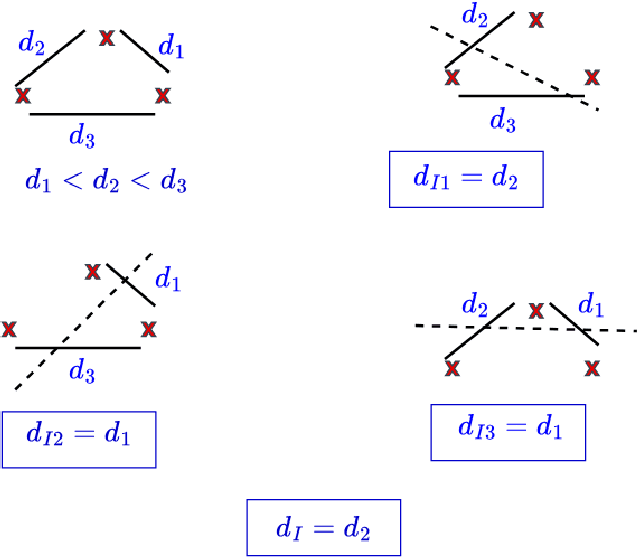
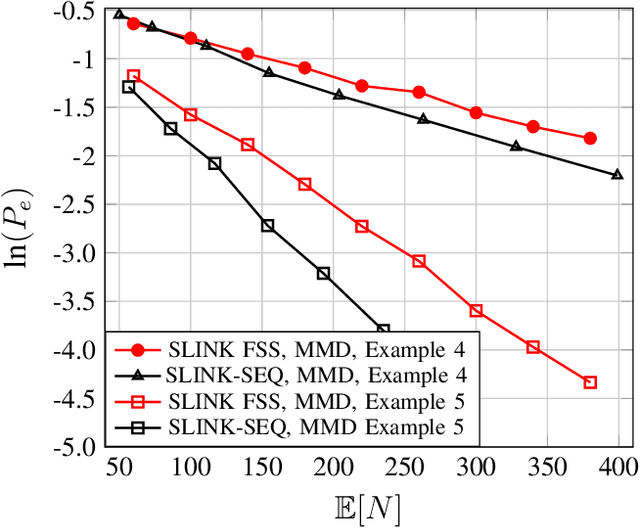
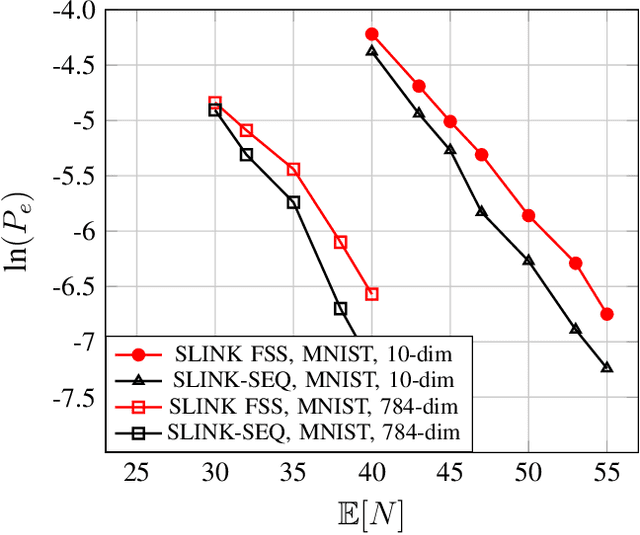
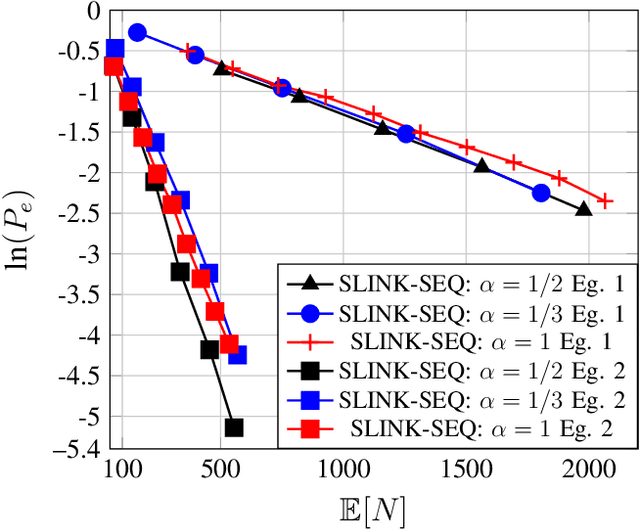
In this paper, we consider nonparametric clustering of $M$ independent and identically distributed (i.i.d.) data streams generated from unknown distributions. The distributions of the $M$ data streams belong to $K$ underlying distribution clusters. Existing results on exponentially consistent nonparametric clustering algorithms, like single linkage-based (SLINK) clustering and $k$-medoids distribution clustering, assume that the maximum intra-cluster distance ($d_L$) is smaller than the minimum inter-cluster distance ($d_H$). First, in the fixed sample size (FSS) setting, we show that exponential consistency can be achieved for SLINK clustering under a less strict assumption, $d_I < d_H$, where $d_I$ is the maximum distance between any two sub-clusters of a cluster that partition the cluster. Note that $d_I < d_L$ in general. Our results show that SLINK is exponentially consistent for a larger class of problems than $k$-medoids distribution clustering. We also identify examples where $k$-medoids clustering is unable to find the true clusters, but SLINK is exponentially consistent. Then, we propose a sequential clustering algorithm, named SLINK-SEQ, based on SLINK and prove that it is also exponentially consistent. Simulation results show that the SLINK-SEQ algorithm requires fewer expected number of samples than the FSS SLINK algorithm for the same probability of error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge