Exponential Step Sizes for Non-Convex Optimization

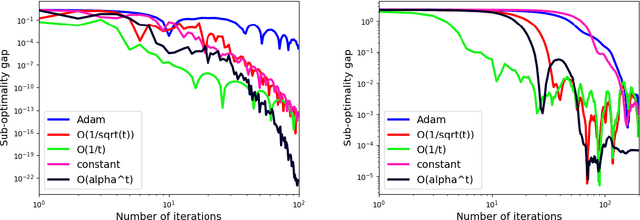
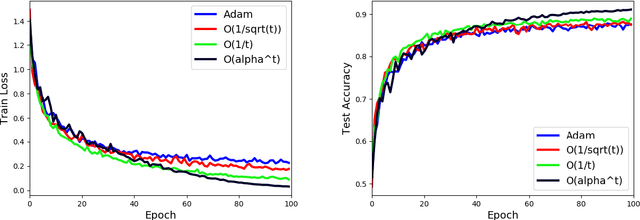
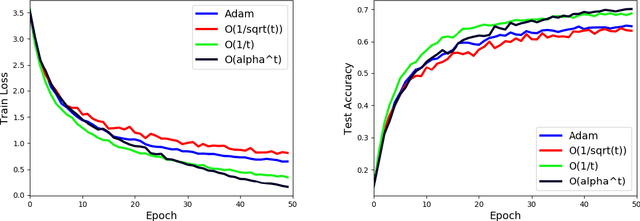
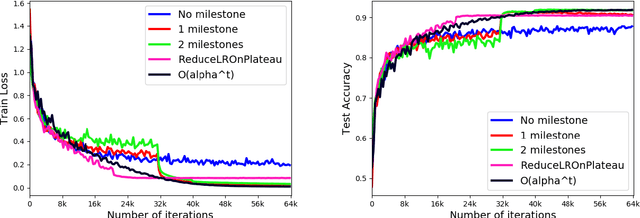
Stochastic Gradient Descent (SGD) is a popular tool in large scale optimization of machine learning objective functions. However, the performance is greatly variable, depending on the choice of the step sizes. In this paper, we introduce the exponential step sizes for stochastic optimization of smooth non-convex functions which satisfy the Polyak-\L{}ojasiewicz (PL) condition. We show that, without any information on the level of noise over the stochastic gradients, these step sizes guarantee a convergence rate for the last iterate that automatically interpolates between a linear rate (in the noisy-free case) and a $O(\frac{1}{T})$ rate (in the noisy case), up to poly-logarithmic factors. Moreover, if without the PL condition, the exponential step sizes still guarantee optimal convergence to a critical point, up to logarithmic factors. We also validate our theoretical results with empirical experiments on real-world datasets with deep learning architectures.