Exploring the Representational Power of Graph Autoencoder
Paper and Code
Jun 22, 2021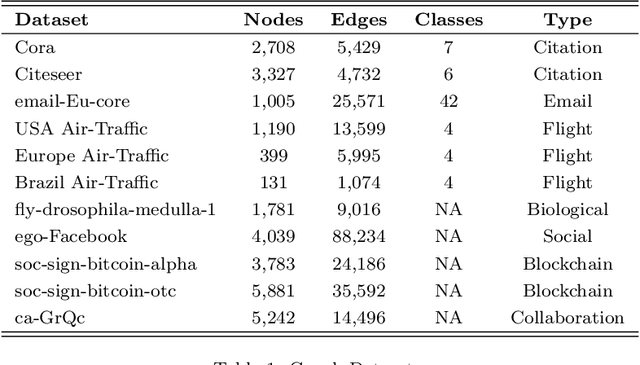
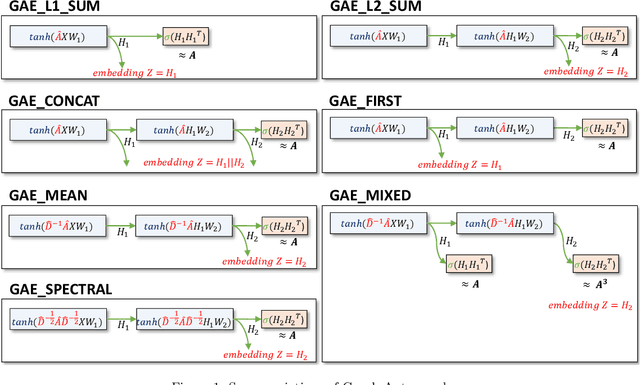
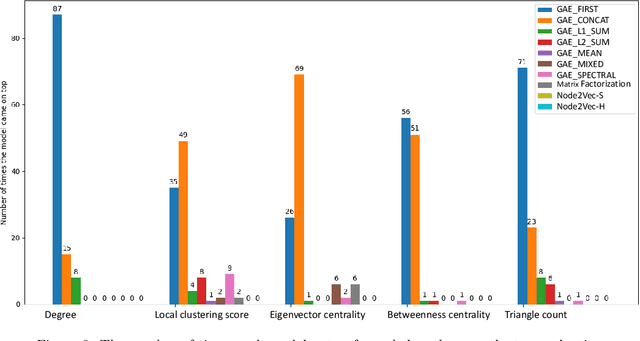

While representation learning has yielded a great success on many graph learning tasks, there is little understanding behind the structures that are being captured by these embeddings. For example, we wonder if the topological features, such as the Triangle Count, the Degree of the node and other centrality measures are concretely encoded in the embeddings. Furthermore, we ask if the presence of these structures in the embeddings is necessary for a better performance on the downstream tasks, such as clustering and classification. To address these questions, we conduct an extensive empirical study over three classes of unsupervised graph embedding models and seven different variants of Graph Autoencoders. Our results show that five topological features: the Degree, the Local Clustering Score, the Betweenness Centrality, the Eigenvector Centrality, and Triangle Count are concretely preserved in the first layer of the graph autoencoder that employs the SUM aggregation rule, under the condition that the model preserves the second-order proximity. We supplement further evidence for the presence of these features by revealing a hierarchy in the distribution of the topological features in the embeddings of the aforementioned model. We also show that a model with such properties can outperform other models on certain downstream tasks, especially when the preserved features are relevant to the task at hand. Finally, we evaluate the suitability of our findings through a test case study related to social influence prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge