Explore the Context: Optimal Data Collection for Context-Conditional Dynamics Models
Paper and Code
Feb 22, 2021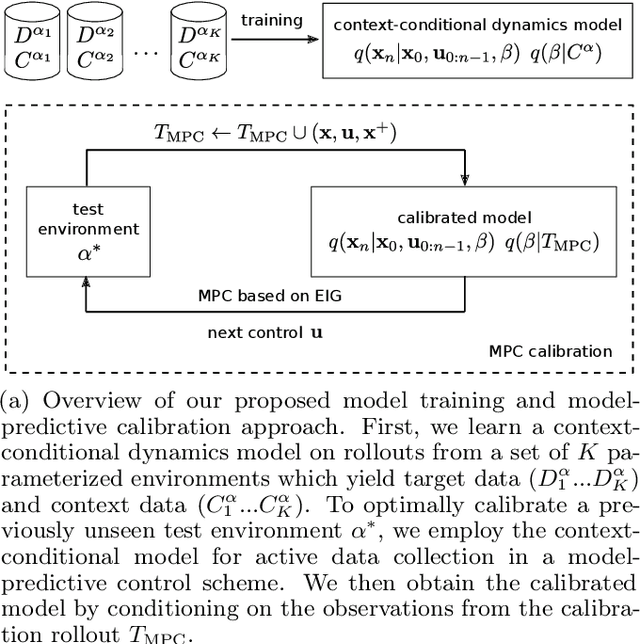
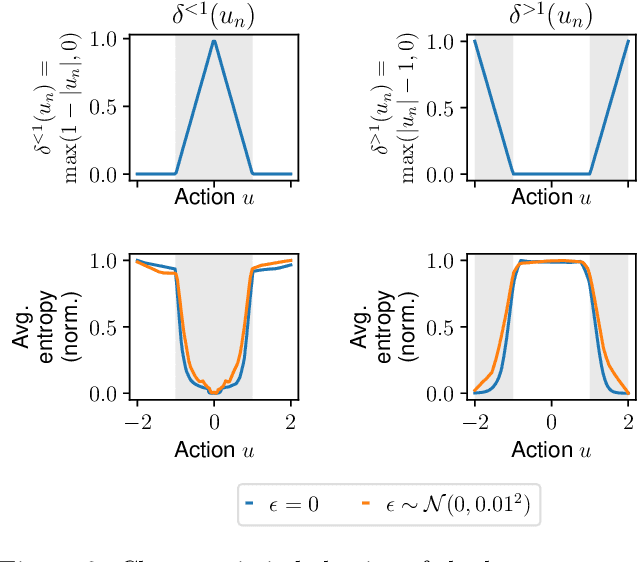
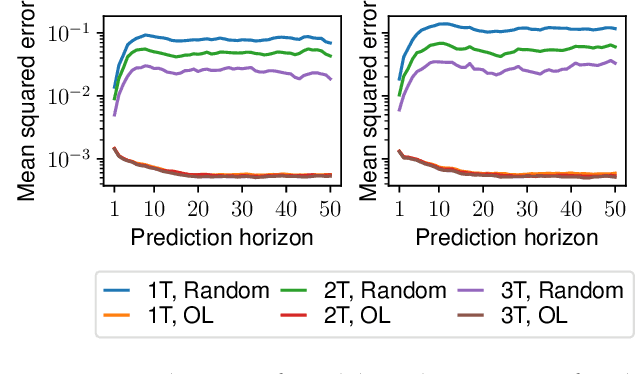
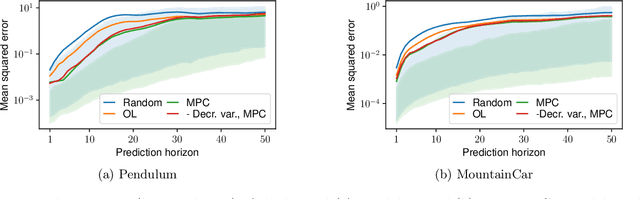
In this paper, we learn dynamics models for parametrized families of dynamical systems with varying properties. The dynamics models are formulated as stochastic processes conditioned on a latent context variable which is inferred from observed transitions of the respective system. The probabilistic formulation allows us to compute an action sequence which, for a limited number of environment interactions, optimally explores the given system within the parametrized family. This is achieved by steering the system through transitions being most informative for the context variable. We demonstrate the effectiveness of our method for exploration on a non-linear toy-problem and two well-known reinforcement learning environments.
* Accepted for publication at the 24th International Conference on
Artificial Intelligence and Statistics (AISTATS) 2021, with supplementary
material
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge