Exploration of Numerical Precision in Deep Neural Networks
Paper and Code
May 03, 2018
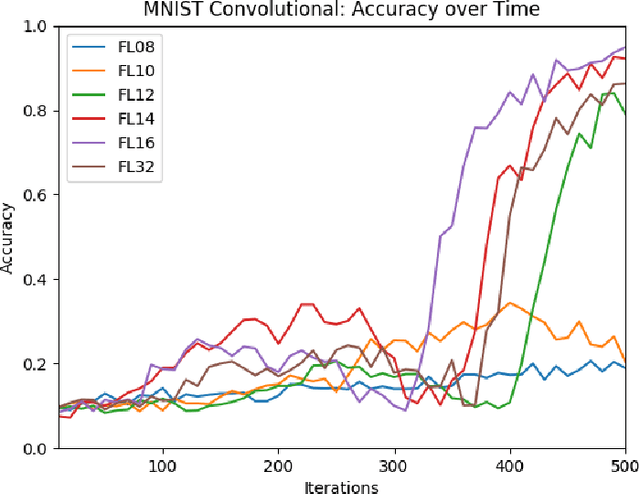
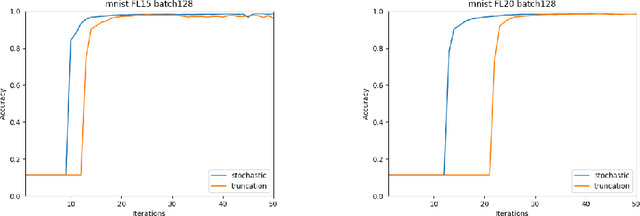
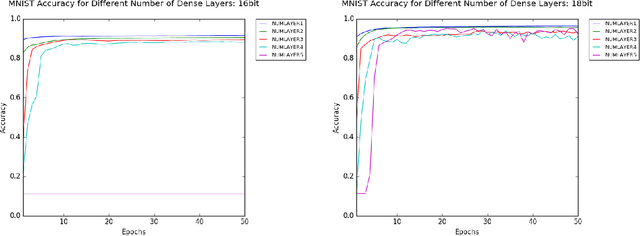
Reduced numerical precision is a common technique to reduce computational cost in many Deep Neural Networks (DNNs). While it has been observed that DNNs are resilient to small errors and noise, no general result exists that is capable of predicting a given DNN system architecture's sensitivity to reduced precision. In this project, we emulate arbitrary bit-width using a specified floating-point representation with a truncation method, which is applied to the neural network after each batch. We explore the impact of several model parameters on the network's training accuracy and show results on the MNIST dataset. We then present a preliminary theoretical investigation of the error scaling in both forward and backward propagations. We end with a discussion of the implications of these results as well as the potential for generalization to other network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge