Exploiting random projections and sparsity with random forests and gradient boosting methods -- Application to multi-label and multi-output learning, random forest model compression and leveraging input sparsity
Paper and Code
Apr 26, 2017
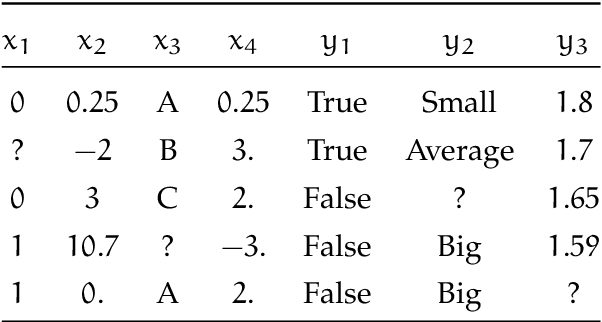

Within machine learning, the supervised learning field aims at modeling the input-output relationship of a system, from past observations of its behavior. Decision trees characterize the input-output relationship through a series of nested $if-then-else$ questions, the testing nodes, leading to a set of predictions, the leaf nodes. Several of such trees are often combined together for state-of-the-art performance: random forest ensembles average the predictions of randomized decision trees trained independently in parallel, while tree boosting ensembles train decision trees sequentially to refine the predictions made by the previous ones. The emergence of new applications requires scalable supervised learning algorithms in terms of computational power and memory space with respect to the number of inputs, outputs, and observations without sacrificing accuracy. In this thesis, we identify three main areas where decision tree methods could be improved for which we provide and evaluate original algorithmic solutions: (i) learning over high dimensional output spaces, (ii) learning with large sample datasets and stringent memory constraints at prediction time and (iii) learning over high dimensional sparse input spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge