Expected Runtime Comparisons Between Breadth-First Search and Constant-Depth Restarting Random Walks

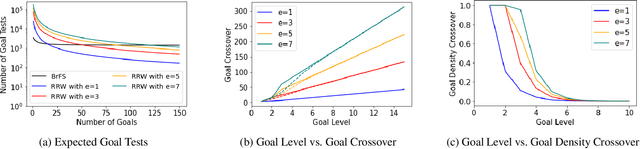
When greedy search algorithms encounter a local minima or plateau, the search typically devolves into a breadth-first search (BrFS), or a local search technique is used in an attempt to find a way out. In this work, we formally analyze the performance of BrFS and constant-depth restarting random walks (RRW) -- two methods often used for finding exits to a plateau/local minima -- to better understand when each is best suited. In particular, we formally derive the expected runtime for BrFS in the case of a uniformly distributed set of goals at a given goal depth. We then prove RRW will be faster than BrFS on trees if there are enough goals at that goal depth. We refer to this threshold as the crossover point. Our bound shows that the crossover point grows linearly with the branching factor of the tree, the goal depth, and the error in the random walk depth, while the size of the tree grows exponentially in branching factor and goal depth. Finally, we discuss the practical implications and applicability of this bound.