Estimation Procedures for Robust Sensor Control
Paper and Code
Mar 27, 2013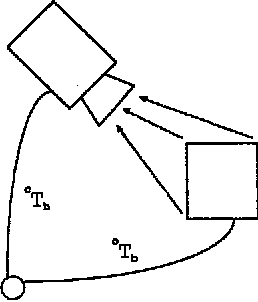
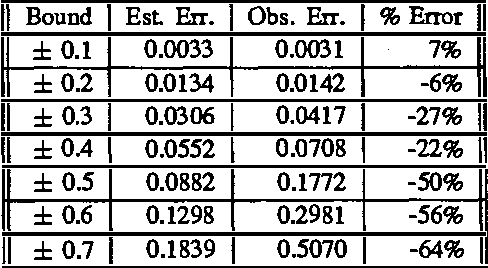
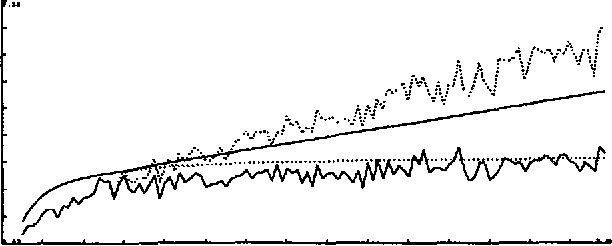
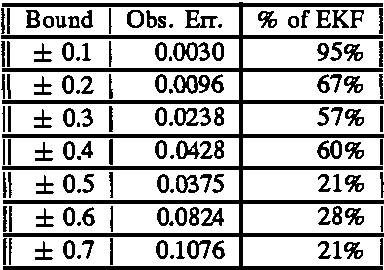
Many robotic sensor estimation problems can characterized in terms of nonlinear measurement systems. These systems are contaminated with noise and may be underdetermined from a single observation. In order to get reliable estimation results, the system must choose views which result in an overdetermined system. This is the sensor control problem. Accurate and reliable sensor control requires an estimation procedure which yields both estimates and measures of its own performance. In the case of nonlinear measurement systems, computationally simple closed-form estimation solutions may not exist. However, approximation techniques provide viable alternatives. In this paper, we evaluate three estimation techniques: the extended Kalman filter, a discrete Bayes approximation, and an iterative Bayes approximation. We present mathematical results and simulation statistics illustrating operating conditions where the extended Kalman filter is inappropriate for sensor control, and discuss issues in the use of the discrete Bayes approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge