Estimating Information-Theoretic Quantities with Random Forests

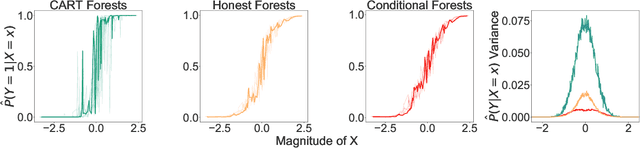
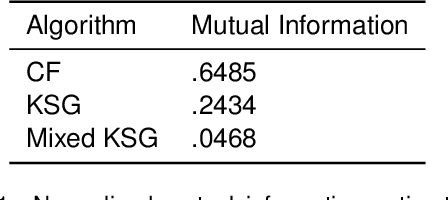
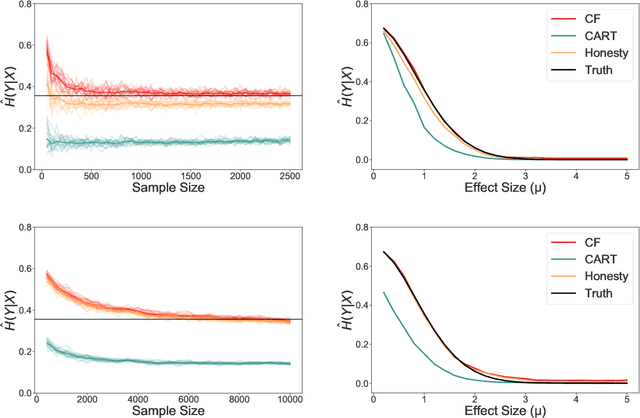
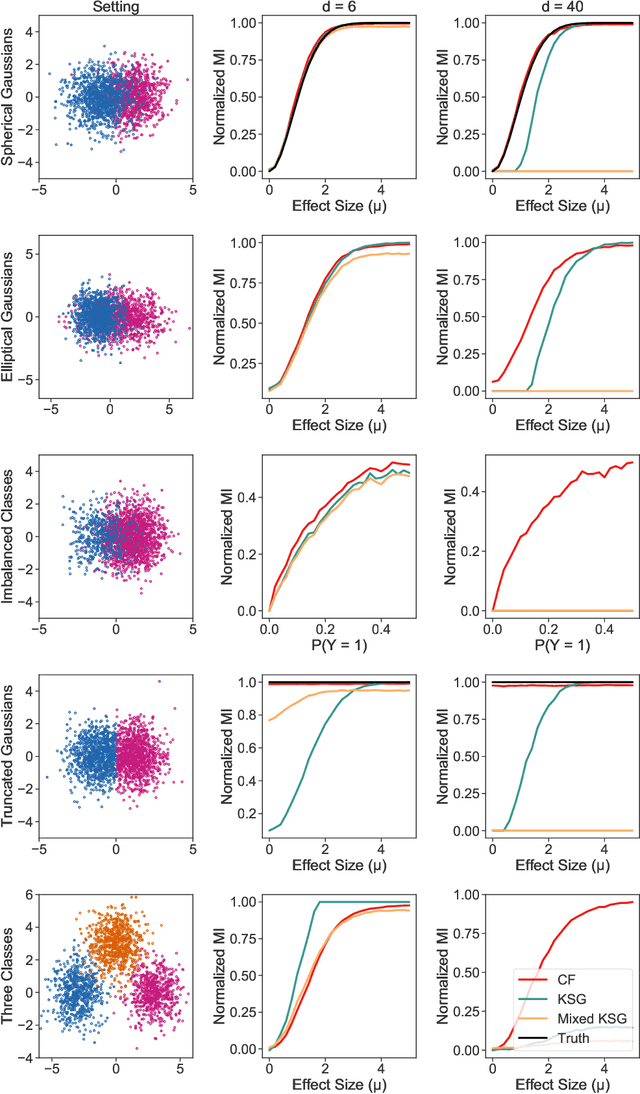
Information-theoretic quantities, such as mutual information and conditional entropy, are useful statistics for measuring the dependence between two random variables. However, estimating these quantities in a non-parametric fashion is difficult, especially when the variables are high-dimensional, a mixture of continuous and discrete values, or both. In this paper, we propose a decision forest method, Conditional Forests (CF), to estimate these quantities. By combining quantile regression forests with honest sampling, and introducing a finite sample correction, CF improves finite sample bias in a range of settings. We demonstrate through simulations that CF achieves smaller bias and variance in both low- and high-dimensional settings for estimating posteriors, conditional entropy, and mutual information. We then use CF to estimate the amount of information between neuron class and other ceulluar feautres.