Estimating decision tree learnability with polylogarithmic sample complexity
Paper and Code
Nov 03, 2020
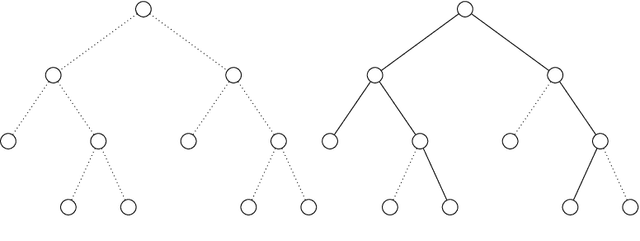
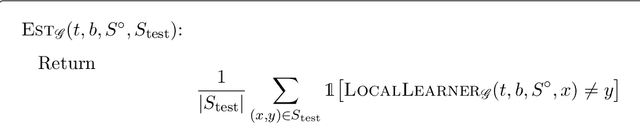
We show that top-down decision tree learning heuristics are amenable to highly efficient learnability estimation: for monotone target functions, the error of the decision tree hypothesis constructed by these heuristics can be estimated with polylogarithmically many labeled examples, exponentially smaller than the number necessary to run these heuristics, and indeed, exponentially smaller than information-theoretic minimum required to learn a good decision tree. This adds to a small but growing list of fundamental learning algorithms that have been shown to be amenable to learnability estimation. En route to this result, we design and analyze sample-efficient minibatch versions of top-down decision tree learning heuristics and show that they achieve the same provable guarantees as the full-batch versions. We further give "active local" versions of these heuristics: given a test point $x^\star$, we show how the label $T(x^\star)$ of the decision tree hypothesis $T$ can be computed with polylogarithmically many labeled examples, exponentially smaller than the number necessary to learn $T$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge