Estimating Causal Effects from Learned Causal Networks
Paper and Code
Aug 27, 2024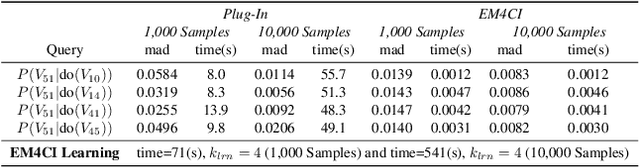
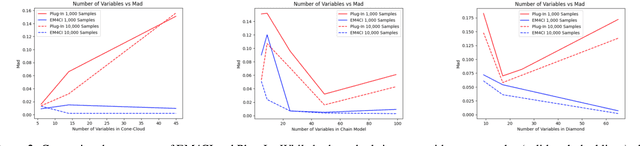
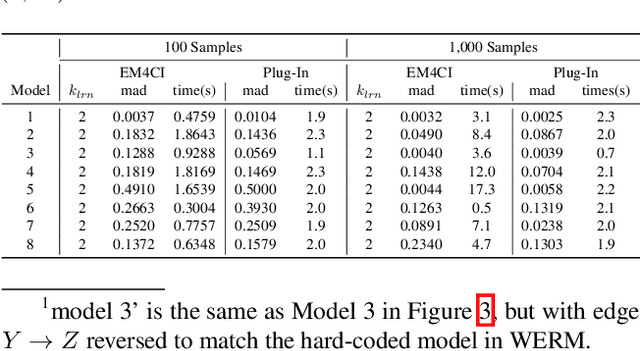
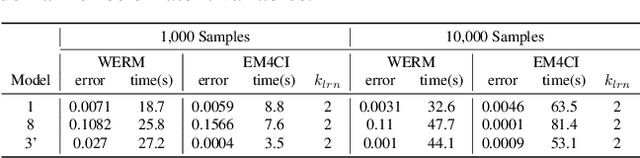
The standard approach to answering an identifiable causal-effect query (e.g., $P(Y|do(X)$) when given a causal diagram and observational data is to first generate an estimand, or probabilistic expression over the observable variables, which is then evaluated using the observational data. In this paper, we propose an alternative paradigm for answering causal-effect queries over discrete observable variables. We propose to instead learn the causal Bayesian network and its confounding latent variables directly from the observational data. Then, efficient probabilistic graphical model (PGM) algorithms can be applied to the learned model to answer queries. Perhaps surprisingly, we show that this \emph{model completion} learning approach can be more effective than estimand approaches, particularly for larger models in which the estimand expressions become computationally difficult. We illustrate our method's potential using a benchmark collection of Bayesian networks and synthetically generated causal models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge