Error Correction in Learning using SVMs
Paper and Code
Jan 10, 2013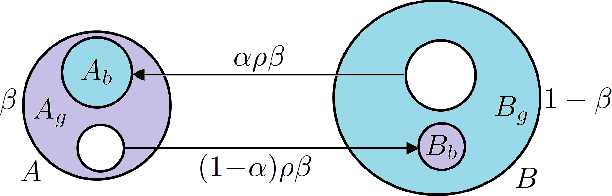
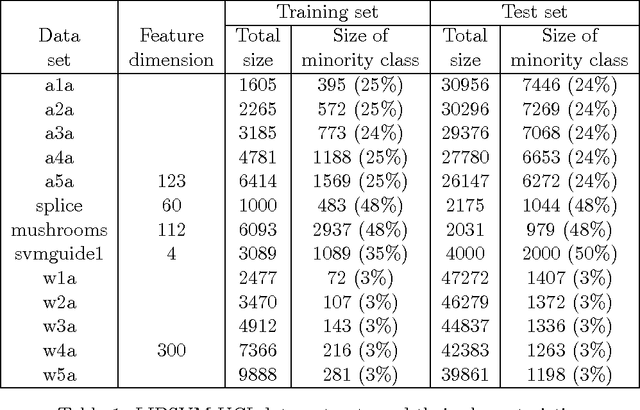
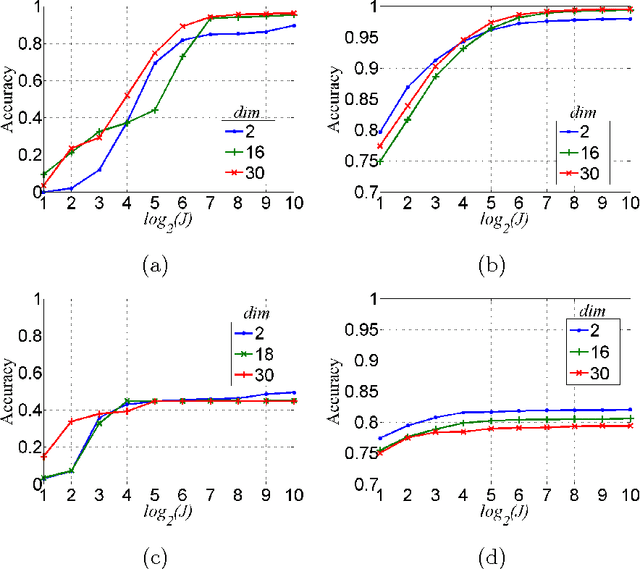
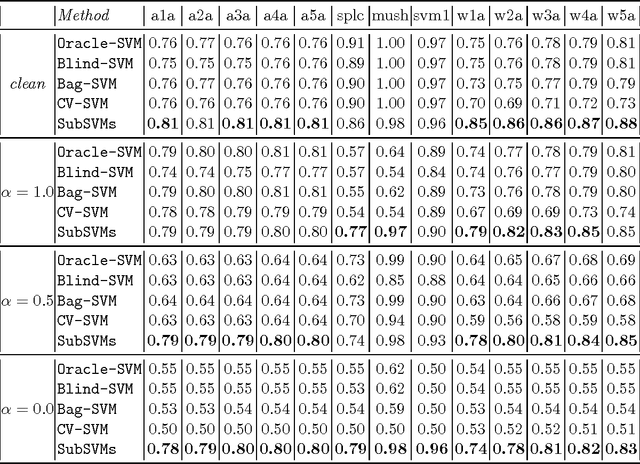
This paper is concerned with learning binary classifiers under adversarial label-noise. We introduce the problem of error-correction in learning where the goal is to recover the original clean data from a label-manipulated version of it, given (i) no constraints on the adversary other than an upper-bound on the number of errors, and (ii) some regularity properties for the original data. We present a simple and practical error-correction algorithm called SubSVMs that learns individual SVMs on several small-size (log-size), class-balanced, random subsets of the data and then reclassifies the training points using a majority vote. Our analysis reveals the need for the two main ingredients of SubSVMs, namely class-balanced sampling and subsampled bagging. Experimental results on synthetic as well as benchmark UCI data demonstrate the effectiveness of our approach. In addition to noise-tolerance, log-size subsampled bagging also yields significant run-time benefits over standard SVMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge