Equity-Directed Bootstrapping: Examples and Analysis
Paper and Code
Aug 14, 2021
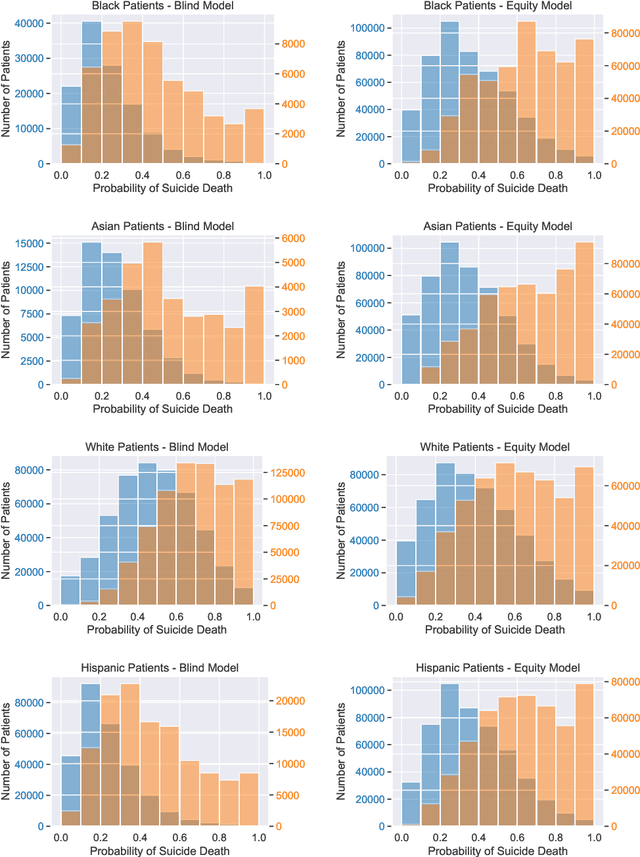

When faced with severely imbalanced binary classification problems, we often train models on bootstrapped data in which the number of instances of each class occur in a more favorable ratio, e.g., one. We view algorithmic inequity through the lens of imbalanced classification: in order to balance the performance of a classifier across groups, we can bootstrap to achieve training sets that are balanced with respect to both labels and group identity. For an example problem with severe class imbalance---prediction of suicide death from administrative patient records---we illustrate how an equity-directed bootstrap can bring test set sensitivities and specificities much closer to satisfying the equal odds criterion. In the context of na\"ive Bayes and logistic regression, we analyze the equity-directed bootstrap, demonstrating that it works by bringing odds ratios close to one, and linking it to methods involving intercept adjustment, thresholding, and weighting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge