Equitability, mutual information, and the maximal information coefficient
Paper and Code
Jan 31, 2013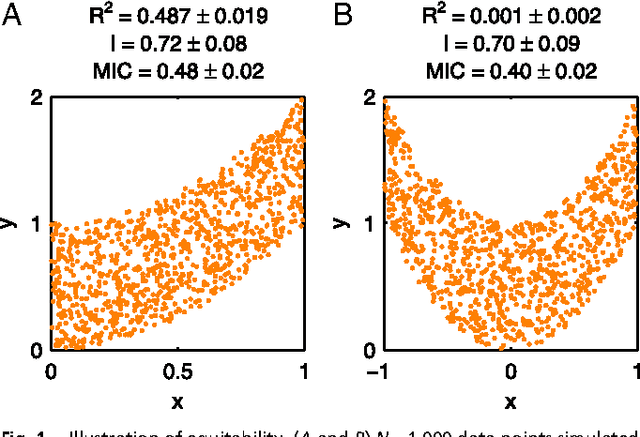
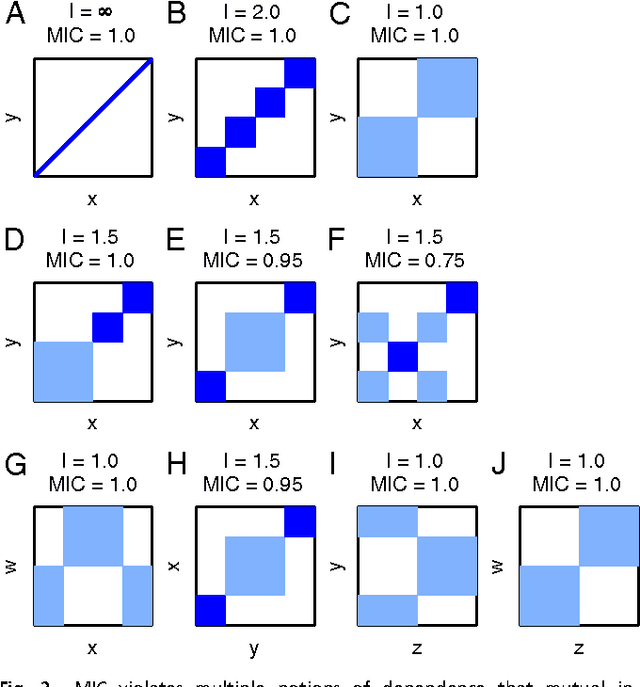
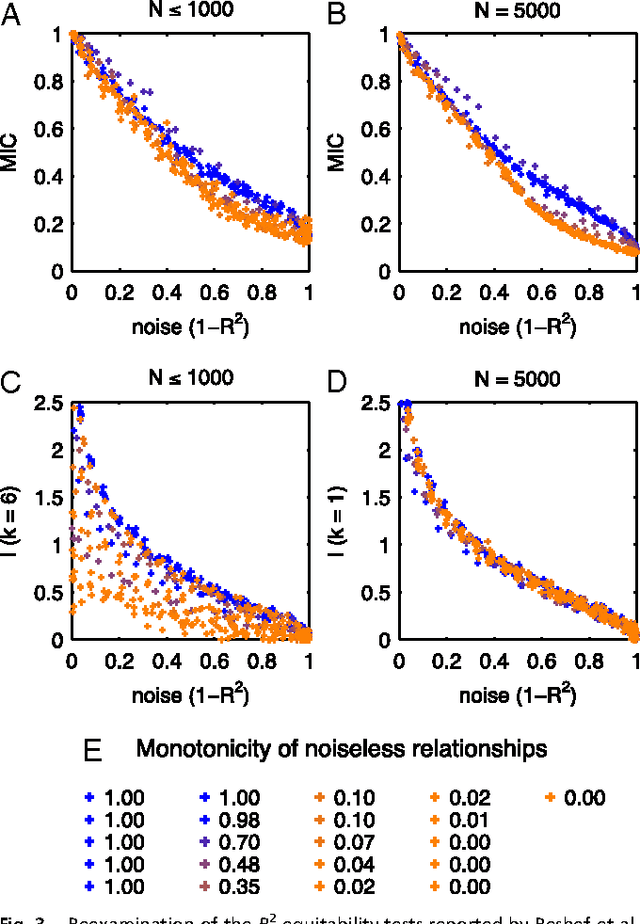
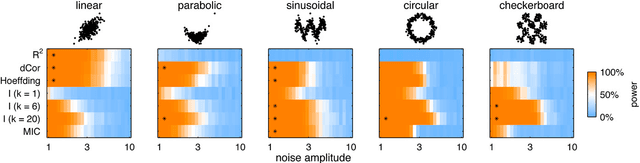
Reshef et al. recently proposed a new statistical measure, the "maximal information coefficient" (MIC), for quantifying arbitrary dependencies between pairs of stochastic quantities. MIC is based on mutual information, a fundamental quantity in information theory that is widely understood to serve this need. MIC, however, is not an estimate of mutual information. Indeed, it was claimed that MIC possesses a desirable mathematical property called "equitability" that mutual information lacks. This was not proven; instead it was argued solely through the analysis of simulated data. Here we show that this claim, in fact, is incorrect. First we offer mathematical proof that no (non-trivial) dependence measure satisfies the definition of equitability proposed by Reshef et al.. We then propose a self-consistent and more general definition of equitability that follows naturally from the Data Processing Inequality. Mutual information satisfies this new definition of equitability while MIC does not. Finally, we show that the simulation evidence offered by Reshef et al. was artifactual. We conclude that estimating mutual information is not only practical for many real-world applications, but also provides a natural solution to the problem of quantifying associations in large data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge